Self-Attention
Self-Attention의 기본 개념
Self-Attention은 기존 RNN + Attention의 단점을 해결하고자 나온 개념이다.
이는 현재 대부분의 LLM의 기반이 되는 트랜스포머의 기본 개념이다.
RNN + Attention에서는 Word Embedding Vector를 기존 RNN 구조에서 계산되는 $h$ 벡터를 사용하였다.
하지만 Self-Attention은 이러한 RNN 구조를 완전히 없애고 인풋의 각 셀마다 각자의 Attention 계산이 들어간다.
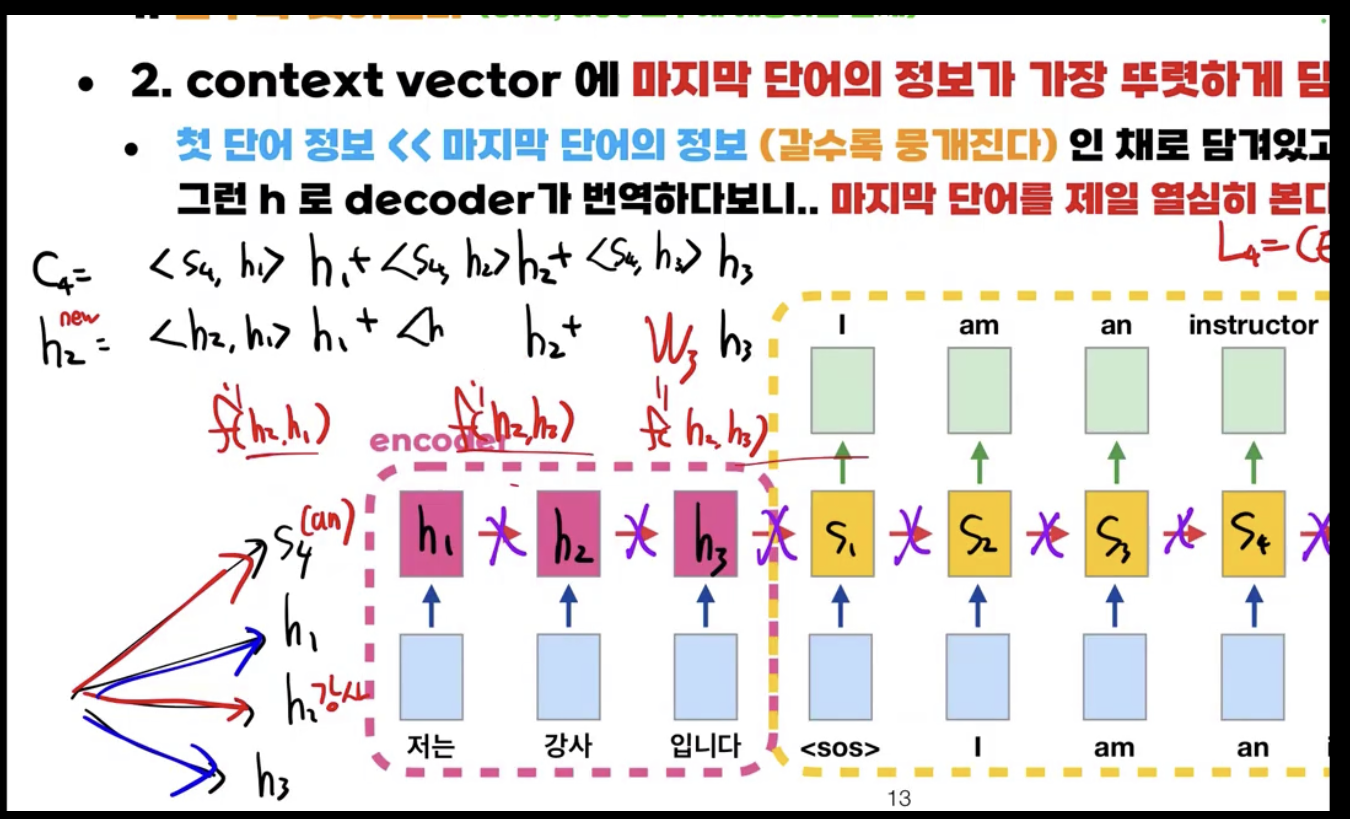
예를 들어 ‘강사’라는 단어의 self-attention vector를 구하는 식은 다음과 같다.
$h^{new}_2 = <h_2,h_1>h_1+<h_2,h_2>h_2+<h_2,h_3>h_3$
이러한 식의 장점은 이전 RNN + Attention의 단점을 얘기할 때 나왔듯이 특정 단어에 따라 의미가 달라지는 단어 같은 경우 각 인풋의 word embedding vector와의 내적을 구해 어느 단어에 따라 해당 단어의 의미가 달리지는지를 파악할 수 있다는 점이다.
또한 거리에 따른 영향을 받지 않을 수 있다.
E-D Attention / Self-Attention / Masked Self-Attention
Self-Attention
$h^{new}_2 = <h_2,h_1>h_1+<h_2,h_2>h_2+<h_2,h_3>h_3$
인코더에 사용되는 Self-Attention 기법이다.
해결점
$h$가 의미를 제대로 담지 못하는 점 해결.
Masked Self-Attention
$s^{new}_4 = <s_4,s_1>s_1+<s_4,s_2>s_2+<s_4,s_3>s_3+<s_4,s_4>s_4+<s_4,s_5>s_5$
디코더에 사용되는 Self-Attention 기법이지만 위의 식은 학습시에만 사용되고 테스트 시에는 다음 항이 Masking 되어 사용되지 않는다.
$s_4$를 기준으로 self-attention을 할 시 테스트 때는 $s_5$에 대한 정보가 없기에 자신의 시점 이후의 셀들은 self-attention을 하지 않는다.
해결점
디코더의 vanishing gradient 문제 해결.
E-D Attention
인코더와 디코더 모두 Self-Attention이 적용된 이후 $c$값을 구할 때 사용되는 Attention 식이다.
$c_4 = <s^{new}_4,h^{new}_1>h^{new}_1+<s^{new}_4,h^{new}_2>h^{new}_2+<s^{new}_4,h^{new}_3>h^{new}_3$
해결점
디코더가 인코더의 마지막 단어를 보는 문제 해결.