RNN 단점 정리
RNN의 Loss 연산
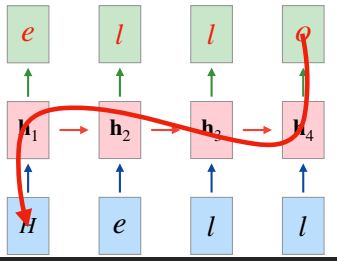
- 다음과 같은 many to many rnn 구조가 있을 때 loss는 cross-entropy로 계산이 된다.
- 각 단계의 출력이 알파벳이기에 다중 분류로 생각할 수 있기 때문이다.
- $L$을 전체 loss라고 하였을 때
$L = \dfrac{L_1+L_2+L_3+L_4}{4}$
라는 식을 생각해볼 수 있다.
Back Propagation의 문제점
- 이제 해당 RNN을 학습할 때 $W_x \leftarrow W_x - \alpha\dfrac{\partial L}{\partial W_x}$ 의 형태로 역전파가 진행될 것이다.
- 그렇다면 전체 loss는 각 블럭 loss의 평균이니 다음과 같은 식이 형성된다.
- $\dfrac{\partial L}{\partial W_x} = \dfrac{1}{4}(\dfrac{\partial L_1}{\partial W_x}+\dfrac{\partial L_2}{\partial W_x}+\dfrac{\partial L_3}{\partial W_x}+\dfrac{\partial L_4}{\partial W_x})$
- 그 중에서 $\dfrac{\partial L_4}{\partial W_x}$는 모든 hidden state를 거쳐 왔기 때문에 weighted sum으로 미분값이 형성이 될 것이다.
- 하지만 H에 해당하는 weight는 tanh의 미분 값을 총 4번이나 곱해지면서 만들어지기에 다른 토큰에 비해 weight가 적어 역전파의 영향을 크게 받지 못할 것이다.
- 즉, 불균형한 weighted sum으로 인해 모든 토큰이 고루 역전파의 영향을 받지 못해 출력에서 먼 토큰은 학습이 잘 되지 않을 것이다.
Forward Propagation의 문제점
- RNN에선 tanh 활성화 함수를 대개들 많이 쓴다.
- 하지만 해당 함수로 인해 정보가 점점 순전파를 진행할수록 뭉개진다.
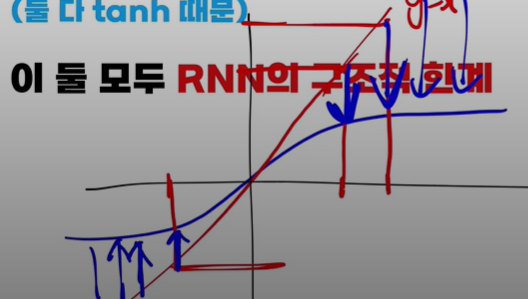
- 빨간 선이 y=x 입력이 그대로 출력되는 경우고 파란 선이 tanh 그래프이다.
- 보다 싶이 y=x 와 달리 tanh를 통과하면 정보가 압축이 되어 RNN 초반에 입력되는 토큰은 순환될수록 정보가 계속해서 뭉개질 것이다.

