RNN and Attention

RNN + Attention

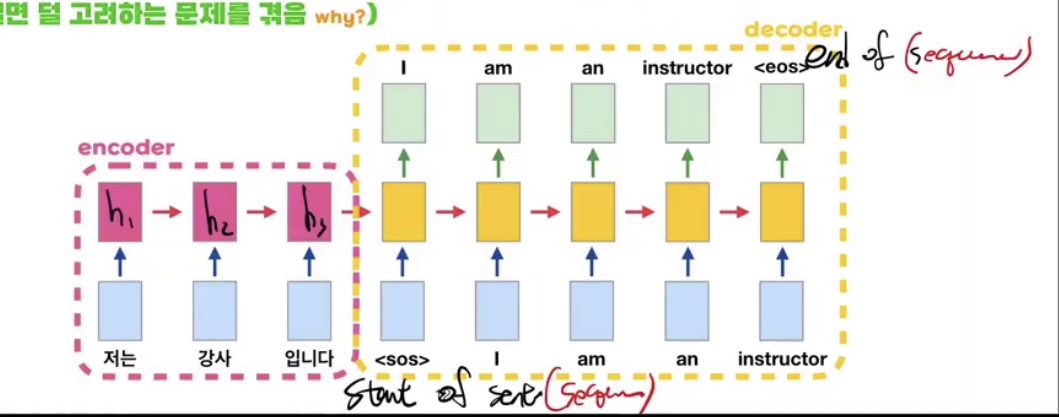
image 13.png

seq2seq의 문제를 해결하기 위해 나온 개념인 Attention이다.
이는 context vector로 $h_3$만을 사용하는게 아니라 각 cell마다 적절한 $h$의 가중치 합을 가져다가 사용한다는 개념이다.
예를 들어 노란색 cell이 $S$라고 가정한다면 기존 라벨을 출력하기 위해서는 다음과 같은 식으로 도출해낼 것이다.
- $\hat{y_4} = s_4W_y+b_y$
하지만 attention을 도입한다면 다음과 같이 식을 바꿀 수 있다.
- $\hat{y_4} = s_4W_y+c_4W_c+b_y$
여기서 $c$가 attention이라는 것이다. $c$는 해당 셀의 가장 중요한 정보를 많이 담고 있도록 집중하도록 해주는 것이다.

위 사진의 인코더를 보면 단어 하나당 하나의 $h$ 벡터가 나오는 것을 볼 수 있다. 이를 Word Embedding Vector라고 말한다.
즉, $h_1$은 ‘나는’ 이라는 단어의 정보를 가장 많이 가지고 있는 Word Embedding Vector인 것이다.
하지만 그러면 여기서 의문은 $h_3$같은 경우는 ‘나는’과 ‘강사’라는 단어의 정보도 가지고 있는데 이는 그저 ‘입니다’라는 단어의 정보를 최대한 많이 담기 위해 참고한다고 보면 된다.
여기서 $c$는 Word Embedding Vector들의 weighted sum이라고 보면 된다.
- $c = w_1h_1+w_2h_2+w_3h_3$
예를 들어 $c_4$는 instructor에 대한 정보를 가장 많이 담고 있어야 되니 $w_2$의 값이 커야할 것이다.

하지만 이 또한 문제점이 있다. 만약 인풋이 “나는 딥러닝 강사입니다.” 이면 강사라는 정보를 많이 담는 벡터는 $h_3$이기에 $w_3$를 키워야 된다. 즉, 인풋에 따라 단어가 같아도 키워야 되는 가중치가 달라질 수도 있다는 것이다.
그래서 Weight를 h의 함수로 두고 디코더에서 어느 시점에 어느 벡터에 집중시켜야되는지를 알기 위해 함수에 S도 포함을 시킨다.
또한, $h$와 $s$의 밀접도를 나타내기 위해 내적을 함수로 사용한다.
즉, $c$에 대한 식은 다음과 같이 바뀐다.
- $c_n = <s_n,h_1>h_1 + <s_n,h_2>h_2 + <s_n,h_3>h_3$
- $<>$는 내적을 뜻한다.
만약 위와 같이 4번째 시점에 대해 $c$를 구한다면 ‘강사’라는 정보를 가장 많이 담은 $h_2$를 키워야되므로 $<s_4,h_2>$가 극대화 되는 쪽으로 학습이 될 것이다.
- 내적의 값이 커질수록 닮음의 정도도 커진다는 것을 기억하자.

$c_n = <s_n,h_1>h_1 + <s_n,h_2>h_2 + <s_n,h_3>h_3$

인코더에서의 잊혀지는 문제는 어느정도 해결이 됐지만 ($c$가 도입됨으로써) 디코더에 대한 정보 잊힘 문제는 아직 해결되지 않았다.
$h$가 의미를 제대로 담고 있지 않다.
- 예를 들어 ‘쓰다’ 라는 단어가 7번째 위치해있고 1번째에 위치한 단어가 ‘돈을’ 혹은 ‘모자를’ 라는 단어가 있으면 1번째 단어에 따라 ‘쓰다’의 의미가 변경이 된다.
- 하지만 $h_7$에는 1번째 단어의 정보가 너무 뭉개진 채로 들어가 있으니 $h$가 의미를 제대로 담고 있지 못한다는 것이다.
- 또한 영어 같은 경우 뒤에 있는 단어를 봐야 의미를 아는 경우도 있는데 이 또한 bidirectional RNN을 사용해야되고 거리에 영향을 받는 다는 것은 여전하다.