Transformer

Transformer - The First Stage

Inputs

• First Stage는 밑의 사진에서 Input Embedding까지의 단계를 말한다.
  • First Stage라는 단어는 인강 자체에서 만든 개념이다.

• 이미지에선 Input을 ‘개채행렬’로 인식을 했다면 NLP에선 ‘개단차’로 인식한다.
• 예를 들어 입력을 다음과 같은 두 문장이라고 하자.
  • 저는 강사 입니다.
  • 저는 딥러닝 강사 입니다.
• 개단차에서 ‘개’는 문장의 갯수를 뜻하기에 위의 예시에선 2가 된다.
• ‘단’은 n개 중에 가장 긴 문장의 단어의 수를 뜻하기에 4가 된다.
  • 하지만 문장마다 길이는 같아야되기에 짧은 문장에는 토큰을 넣어준다.
• ‘차’는 임베딩 차원으로써 트랜스포머에선 512차원을 쓴다.
• 즉, 예시에서 개단차는 2x4x512이다.

Input Embedding

• 입력 문장을 받은 이후 컴퓨터는 우리가 쓰는 자연어를 그대로 이해하지 못하기에 이해할 수 있도록 숫자 벡터로 임베딩을 해줘야 한다.
• 맨 처음 inputs은 원-핫 형태로 존재한다. 예를 들어 ‘저는 강사 입니다.’ 가 인풋이라고 해보자.
  • 저는 = [0 0 0 0 … 1 … 0 0 0] → 1482번째만 1, 나머지는 0
  • 강사 = [0 0 0 0 0 0 … 1 … 0 0] → 5821번째만 1, 나머지는 0
  • 입니다 = [0 … 1 … 0 0 0 0 0] → 243번째만 1, 나머지는 0
• 해당 인풋은 7851 차원으로 이루어져 있는데 이는 예시일 뿐이고 7851인 해당 예시의 어휘 크기이다.
  • 즉, 내가 써먹을 수 있는 한글 단어의 총 개수이다.
• 이후 nn.Linear(7851, 512)를 통과하여 개x단x512의 형태로 임베딩이 되는 것이다.
  • 해당 행위는 임베딩 행렬을 통과하는 것으로 임베딩 행렬은 7851 x 512의 형태를 가지고 있을 것이다.
  • 7851개에 대한 단어의 랜덤 512차원 백터값이 들어있는 행렬이며 해당 행렬이 학습이 되어 비슷한 단어끼리는 비슷한 벡터 값을 가질 수 있도록 하는 것이다.
  • 어휘 크기나 임베딩 차원 크기는 trade-off 형식으로 커질수록 연산량이 커지지만 성능은 높아진다. 즉, 환경에 따라 조절하면 되는 하이퍼파라미터인셈이다.
• 또한, nn.Linear 처럼 fc layer를 통과하는게 아니라 입력 값이 개, 단으로만 이루어져있고 1이 어디에 있는지 인덱스 값만 넘겨줘도 임베딩이 가능하다.
  • 해당 명령은 nn.Embedding으로 파이토치에서 구현 가능하다.

Positional Embedding

• 기존 RNN + Attention 구조에서는 cell들이 연결되어 있기 때문에 단어의 위치 정보를 알 수 있지만 Transformer의 경우 연결되어 있지 않고 독립적으로 self-attention을 시행하기 때문에 위치 정보가 필요하다.
• 위치 정보를 주기 위해 Positional Embedding을 실시한다. 모델에 통과시킬 최대 문장의 길이를 직접 선정해주고 그만큼의 길이로 각 위치 별 원핫 인코딩을 해준다.
  • 예를 들어 1번째 위치면 [1 0 0 0 0 0 … ] 이런 식으로 말이다.
• 이후 nn.Linear(max_len, 512) 로 512차원으로 임베딩을 해주고 이 또한 위의 워드 임베딩과 같이 학습이 되는 임베딩 행렬을 가진다.

• 최종적으로 Input Embedding을 통과한 워드 임베딩 벡터와 위치 임베딩 벡터를 더함으로써 self-attention 을 할 준비가 완료 되는 것이다.

Transformer - The Second Stage

Scaled Dot Product Attention

• Transformer의 경우 워드 임베딩 벡터와 위치 임베딩 벡터가 합쳐진 최종 입력 값을 QKV라는 벡터로 변환한다.
• Q = Query, K = Key, V = Value 로써 각자의 역할이 정해져 있다.
  • Query : 내가 찾고 싶은 정보에 대한 벡터
  • Key : 다른 단어들이 제공하는 정보에 대한 벡터
  • Value : 실제로 가져올 정보
• QKV는 다음과 같은 선형 변환으로 인해 계산된다.
  • $Q = XW^Q$
  • $K = XW^K$
  • $V = XW^V$
  • 여기서 X는 최종 인풋을 말한다. (워드 임베딩 + 위치 임베딩)
  • 각 가중치 행렬들은 학습이 가능한 행렬이다.
  • 또한 해당 선형 변환 이후 차원 수가 줄어드는게 보편적이다. (예시에선 512차원에서 64차원으로 축소한다.)
    • 줄어드는 이유는 Multi-Head Attention을 위해서인데 이는 나중에 설명하겠다.
• 선형 변환으로 나온 Q, K, V 벡터는 다음과 같은 연산이 진행된다.
  • $Attention(Q,K,V) = softmax(\dfrac{QK^T}{\sqrt{d^k}})V$
  • Q와 K 벡터를 내적하여 각 단어마다 다른 단어들과의 내적을 구해 유사도를 계산한다.
  • 이후 차원 수의 제곱근으로 내적 값을 scale 해준다.
    • scale이 들어가는 이유는 차원 수가 크면 분산이 커져 미분 값이 작아지며 softmax 연산 값이 너무 한쪽에 치중되어 학습이 어려워지기 때문이다.
  • 이후 softmax를 통해 각 내적 값의 합이 1이 되며 양수가 되도록 하고 최종적으로 V 벡터와 곱하여 Self-Attention 값을 구하는 것이다.

Multi-Head Attention

• 위의 Scaled Dot Product Attention에서 512차원을 64차원으로 축소하여 QKV 선형 변환을 진행하였다.
• 즉, 8배 축소를 했기 때문에 똑같은 연산을 8번 진행을 하여 8개의 64차원 임베딩 벡터를 내놓을 것이다.
• 이를 Horizontal Concat. 하여 다시금 512차원의 벡터로 만든다.
• 그러면 애초에 nn.Linear(512,512)를 하면 되지 왜 굳이 8개로 쪼개서 다시 합치느냐?
  • 집단 지성의 힘이다. 정보의 다양성을 늘려 성능을 올리려는 것이다.
  • 파라미터 갯수도 변화는 없다. nn.Linear(512,64) x 8 이나 nn.Linear(512,512) 1개나 수는 같다.
• Concat. 이후 Linear(512,512)를 다시 한번 통과하는데 그 이유는 서로 모은 8개의 64차원 벡터의 정보를 조합하여 의견 교류를 하기 위함이다. 그냥 이어져 있다고 정보가 서로 교류되는게 아니기 때문이다.

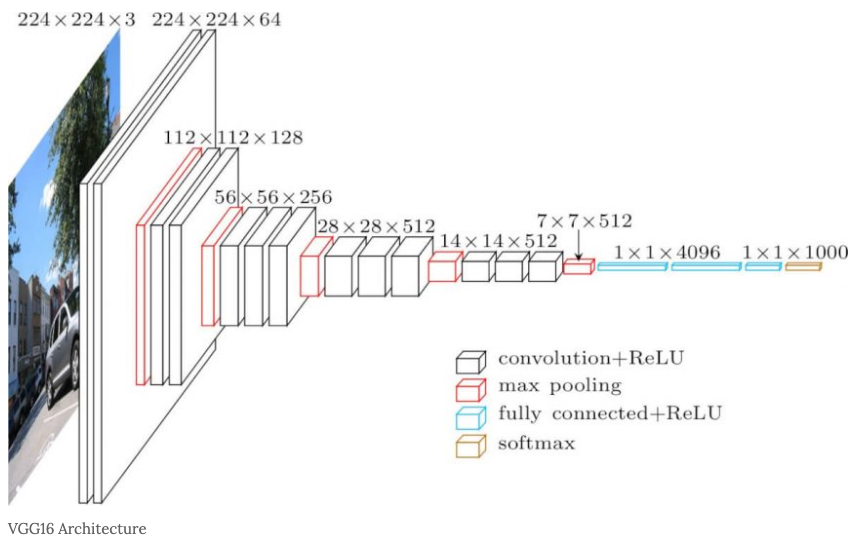
Encoder 전체 구조

• 다음 구조가 전체적인 Encoder의 구조이다.
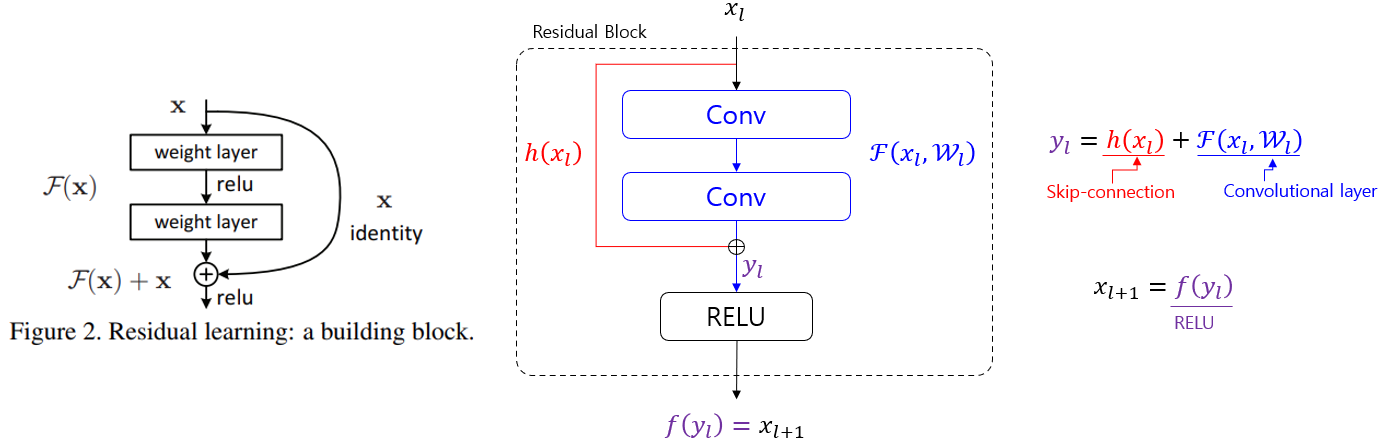
• Multi-Head Attention의 연산이 끝나면 Skip-Connection을 통해 단차를 학습한다.
  • Skip-Connection은 정보의 손실을 줄일 수도 있지만 항등 함수를 학습함으로써 학습을 급진적이 아니라 천천히 학습하게 해준다.
• 이후 Layer Normalization을 통해 기울기 손실 문제를 해결한다.
• 이후 FFN (Feed Forward Network)를 통과하는데 이는 다음과 같은 구조를 띈다.
  • nn.Linear(512, 2048) nn.ReLU() nn.Linear(2048, 512)
  • MobileNet V2에서 쓰였던 기법이며 채널을 늘리고 줄이는 사이에 비선형 활성화 함수를 넣어 비선형성을 늘리며 표현력을 증가시킨다.
  • 또한 다시 채널 수를 줄이며 연산량을 줄인다.
• 이후 동일하게 Skip-Connection과 Layer Normalization을 시행한다.
• 해당 과정을 6번을 거치는것이 Encode

Encoder 구조 분석

• Multi-Head Attention은 단어끼리의 관계를 학습하는 블럭이라고 보면 된다. 즉, 세로의 연산이 들어가는 계산 과정이다.
• 하지만 FFN 즉, MLP는 가로의 연산이 들어가는 것이다. 해당 연산은 하나의 단어만을 보고 연산을 하는 것인데 이게 굳이 필요할까?
  • 단어와 단어의 관계성이 문장의 의미를 파악하는게 중요한거지 단어 하나의 의미를 아는게 중요할까? 라는 접근인거다.
  • 하지만 MLP가 없으면 성능이 떨어지는 경우가 보였고 MHA로 단어의 관계성을 파악하고 FFN으로 단어 의미를 강화하는 것이 좋다는 결론에 다다랐다.
  • 여담으로 Skip-Connection을 없애면 성능이 대폭 저하한다는 것도 밝혔다. (Kaiming He 그는 신인가…)

Masked MHA

• seq2seq과 같이 트랜스포머도 teacher forcing을 사용한다.
• 학습 시에는 디코더에서 정답을 미리 넣어주지만 테스트 시에는 출력된 결과물을 가지고 다음 입력으로 사용한다.

• 그러면 어떻게 Masking이 진행되느냐?

  

  

  • 자신까지만 정보를 볼수 있고 그 이후 정보는 매우 작은 음수로 바꿔져 softmax를 통과하면 0으로 처리 된다.
  • 그러면 그냥 softmax 이후에 0으로 바꾸면 되지 않을까?
    • 안된다. 그러면 가로의 합이 1이 되지 않아 정보가 손실된다.

Encoder-Decoder Attention

• 이제 디코더에서 어떻게 인코더의 정보를 받아오냐에 대한 단계이다.
• 해당 단계를 Encoder-Decoder Attention이라고 부른다.
• Decoder도 동일하게 Input Embedding과 Position Embedding 단계를 거친 후 Masked MHA를 한단계 먼저 거친다. (물론 Skip-Connection과 LN은 포함이다.)
• 이후 Q값은 디코더 자체에서 얻은 값으로 K,V는 인코더에서 얻은 값으로 MHA를 실행한다.
  • 여기서 K,V는 6번의 순환을 다 거친 인코더의 최종 결과물이다.
• 디코더 블럭 또한 인코더와 동일하게 총 6번의 순환을 돈다.
• FFN 경우도 인코더와 동일하게 시행이 된다.

Transformer - The Last Stage

결과 출력

• 6번을 다 거친 최종 디코더의 출력을 선형 변환을 통해 5972차원으로 늘려준다.
  • nn.Linear(512,5972)
  • 왜 5972냐? 하면은 영어 어휘의 크기가 5972로 정의해서 그렇다.
• Softmax를 거쳐 각 확률을 구하고 가장 높은 확률을 택함으로써 추론 시 단어가 나온다.
• Image Classification과 비슷하다고 생각하면된다.

실제 추론 과정

• 추론 시에는 인코더는 딱 한번만 (총 6회) 실시 되고 이후에는 순환되지 않는다.
• 먼저 가 디코더에 들어가고 6번의 순환 후에 예측한 다음 단어를 내놓는다.
• 이후 와 예측한 단어가 들어가고 6번의 순환 후 다음 단어를 예측한다.
• 해당 과정이 가 나올 때 까지 반복된다.
• 추론 시에도 똑같이 masking이 적용된다.

Beam Search

• 추론 시에는 softmax에서 가장 높은 확률의 단어를 고르는 것이 아니라 beam search라는 방법도 실시하기도 한다.
• Beam Search는 추론 단어 후보들 중 확률이 높은 3개의 단어를 고르고 트리 형식으로 쭉 3개씩 뽑아 그중에서 가장 확률이 높은 조합을 찾는 것이다.

Dropout

• 논문에서는 총 7번의 드롭아웃을 하였다.
• 드롭아웃 확률은 p = 0.1로 통일하였다.
• 논문은 V5까지 총 5번의 수정이 있었는데 V4 까지는 어텐션 안에서도 드롭아웃이 적용되었었다.
• 어텐션에서의 드롭아웃은 다음과 같은 의미를 갖는다.
  • 문장 단어 중 하나가 없을 때 너는 이 단어를 뭐라고 해석하고 추론할 것인가?
• FFN이나 Skip-Connection에서의 드롭 아웃은 본래의 목적 처럼 오버피팅 방지라고 생각하면 될 것 같다.

트랜스포머의 목적 및 방향성

• 결국 트랜스포머는 임베딩 벡터를 어디에 위치시킬 지를 학습하는 것이다.

• 좌측이 학습 이전이라면 우측이 학습 이후의 임베딩 벡터의 모습이다.
• 단어의 의미와 문맥에 따라 어느 단어와 밀접한지를 벡터의 위치를 조정하며 학습하는 것이다.
• 이때 중요한 점은 트랜스포머는 Skip-Connection이 많은 부분을 차지하고 있기에 급진적으로 변하는 학습이 아니라 항등함수를 학습함으로써 조금씩 점진적으로 ‘톡톡’ 벡터를 쳐내면서 이동시키며 학습을 시키는 것이다.
  • 즉, 차이 벡터만을 학습하는 것.
• 또한, 추론 시에도 임베딩 벡터는 위치가 달라지는데, 예를 들어 ‘쓰다’라는 단어는 문맥에 따라 의미가 다양한 단어이다. 해당 단어같은 경우 추론 시 입력 문장에 따라 의미가 달라지기에 추론 시에 개인의 입력에 맞춰 임베딩 위치가 달라지고 점점 개인화가 되어 간다.
  • 예를 들어 GPT의 답변이 사람마다 다르며 지난 답변과 내가 입력하던 내용에 따라 단어의 의미도 자기가 알아서 수정하는 것이다.
  • 이것이 트랜스포머의 놀라운 점이며 엄청난 활용점인 것이다.
  • 개인화 AI의 시대가 열리는 것.