SENet (2017.09)

등장 배경

  • SENet은 피처 맵에서 채널 간의 관계성에 주목하여 만들어진 모델이다.
  • 기존 Convolution도 채널 간의 관계성을 고려하지만 이보다 더 explicit하게 관계성을 네트워크에 추가해준다는 것이 SENet의 핵심 아이디어이다.
  • SENet은 ILSVRC-2017에서 DenseNet을 제치고 1등을 차지하였다.

논문 출처

1709.01507

채널 간의 관계성

  • 채널 간의 관계성 혹은 Channel Dependency는 물론 기존 Convolution 구조에서도 고려한 요소이다.
  • 해당 정보는 각 채널들이 보관하고 있는 특성이 이미지를 식별하는데에 얼마나 중요한가를 구별할 수 있는 요소이다.
  • 먼저 논문에서는 Convolution 연산을 $F_{tr}$이라고 가정하고 (BN, ReLU도 포함된 것이다), $F_{tr}$을 통과하여 나온 피처맵을 $U$, 그리고 커널을 $V$라고 하였다.
  • 또한, $U$와 $V$를 채널로 나누어 $U = [u_0,u_1,\cdots,u_c]$ 그리고 $V = [v_0, v_1, \cdots, v_c]$ 의 형태로 나타내었다.
  • 논문의 작성 방식을 따라 기존 Convolution을 식으로 나타내보자면…
    • $u_c = v_c * X = \sum\limits_{s=1}^Cv^s_c*x^s$
    • 위 식에서도 보다싶이 채널 간의 관계성을 summation으로 표현하며 implicit하게 정보를 전달해주었다.
    • 또한, 채널 전체의 정보를 보는 것이 아니라 local 하게 보기 때문에 local spatial correlation 정보와 entangle 되어 온전한 채널의 정보가 넘어가지 않는다.
  • 이를 문제점으로 삼은 SENet 논문의 저자들은 채널 간의 관계성이라는 정보를 어떻게 explicit하게 넘길까라는 고민을 하게 된다.

Squeeze-Excitation (SE)

  • 채널 관계 성을 도출해내기 위해 SE 라는 새로운 모델 아키텍쳐를 제안한다.

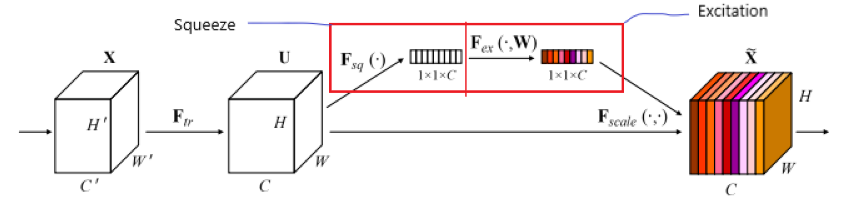
image 4.png

(1) Squeeze

  • Squeeze는 단어 뜻대로 압축을 하는 단계이다. 피처 맵의 각 채널에 있는 정보를 압축하여 채널을 대표하는 channel descriptor $z$를 만드는 과정이다.
  • Squeeze는 다음과 같이 계산된다.
    • $z_c = F_{sq}(u_c) = \dfrac{1}{H+W}\sum\limits_{i=1}^H\sum\limits_{j=1}^Wu_c(i,j)$
    • 각 채널에 있는 피처 맵의 pixel-wise sum을 구한 뒤 피처 맵의 사이즈로 나눈다.
    • 즉, Squeeze는 Global Average Pooling, GAP와 같은 연산이다.

(2) Excitation

  • Excitation 과정은 GAP를 통해 만들어진 channel descriptor를 가지고 channel-wise dependencies $s$를 구하는 연산 과정이다.
  • 채널 간 관계성을 구하는 연산에서는 2가지 기준을 맞춰야 된다고 논문에서는 서술한다.
    1. 연산 과정은 flexible 해야한다. 즉, non-linearity가 추가되어야 한다는 말이다.
    2. Non-mutual Exclusive Relationship을 학습해야한다. ReLU와 같이 0 아니면 1이 아니라 연속적인 값으로 관계성을 도출해내서 여러 채널 사이의 관계성이 나와야 된다는 말이다.
      1. 이에 대한 추가적인 이유는 최대한 여러 채널을 강조하기 위해서 라고 서술한다.
  • 위에서 언급한 2가지 기준을 맞추기 위해 Excitation 과정에선 1번을 위해 ReLU를 사용하고 2번을 위해 sigmoid를 사용한다.
  • Excitation은 다음과 같이 계산된다.
    • $s = F_{ex}(z,W) = \sigma(g(z,W)) = \sigma(W_2\delta(W_1,z))$
    • 즉, 두 단계의 MLP를 거치는 과정이며 첫 MLP에선 ReLU를 사용하고 두번째 MLP에선 Sigmoid를 활용한다.
  • 이후 계산된 $s$는 각 채널에 대응하는 $U$ 피처 맵에 스칼라 곱으로 weight가 곱해진다.

SE Block에서의 Bottleneck 구조

  • 여태 논문에서 봤듯 이제는 게산 효율성을 위해 Bottleneck 구조가 필수적으로 자리를 잡은 것 같다.
  • SE 연산 과정 내에서도 Bottleneck 구조가 도입되었는데 이는 Excitation 구조에 도입되었다.
  • 두번의 MLP 과정 중 C개의 채널에서 C/r 개의 채널로 줄인 뒤 다시 C개의 채널로 늘리는 구조가 도입 되었다. 여기서 r은 reduction ratio이며 이는 하이퍼 파라미터로써 사용자에 의해 조절이 가능하다.

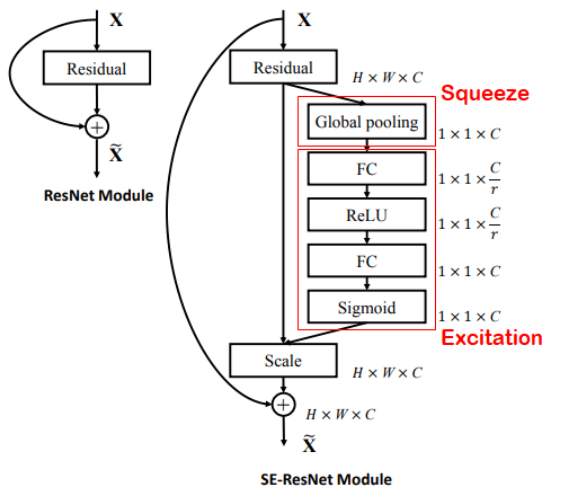
image.png

  • 다음 그림과 같이 첫 FC에선 C⇒ C/r 그리고 두번째 FC에선 C/r ⇒ C로 채널 수가 변경된다.

SE Block의 Flexibility

  • 사실 SENet이라는 이름 자체가 오류이다. 해당 논문에서 제안한 방식은 새로운 블럭이지 네트워크 그 자체가 아니기 때문이다.
  • SE Block의 가장 큰 장점 중 하나는 어느 네트워크이든 적용할 수 있다는 것이다.
  • 이에 대한 예시로 SE-Inception과 SE-ResNet 그리고 SE-ResNeXt등 논문에서 많은 모델을 실험해보았다.

SE Block의 성능 개선 효과

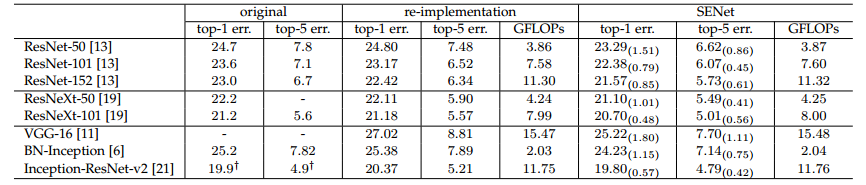
image.png

  • 해당 테이블을 보면 전반적으로 SE를 적용한 것이 성능이 더 높게 나온 것을 볼 수 있다.
  • 하지만 여기서 들 수 있는 의문점이 하나 있다. SE를 부착함으로써 연산량이 올라갔으니 성능이 올라가는 건 당연한거 아닌가?
    • 물론 이는 맞는 말이다. 하지만 효율성이 다르다.
    • ResNeXt-50과 ResNeXt-101의 성능을 비교하자면 ResNeXt-101이 top-1 error 기준 0.93%의 성능 개선을 보여주었다.
    • 하지만 ResNeXt-50에 SE를 부착하면 성능이 1.01%가 올라간다.
    • GFLOPS를 보자면 깊이를 101층으로 늘린 것은 거의 2배가 올랐지만 SE를 부착한 것은 고작 0.01 GFLOPS가 오른 반면 성능은 더 개선되었다.

Ablation Study

  • 어째서 SE 구조가 위와 같이 만들어졌는지에 대한 실험들이다.

(1) Max Pooling vs. Avg. Pooling

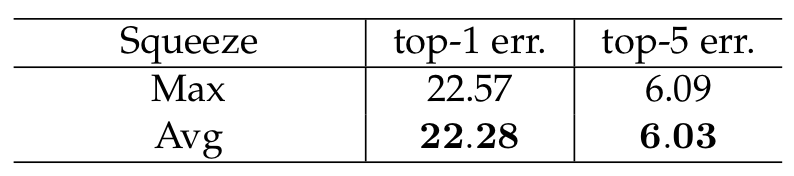
image.png

  • 둘 다 적용해보았을 때 Avg. Pooling의 성능이 더 좋게 나와 Squeeze 과정에서 GMP가 아닌 GAP를 채택하였다.

(2) Reduction Ratio

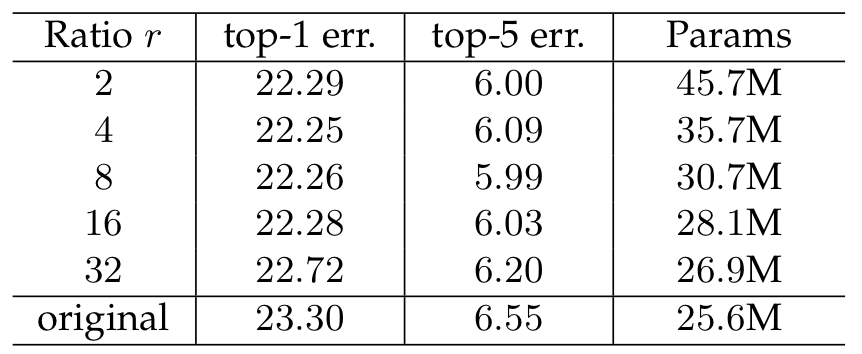
image.png

  • 논문에선 Reduction Ratio를 16을 사용하였는데 그 이유는 그게 가장 성능이 잘 나와서 라고 한다.

(3) Excitation Operator

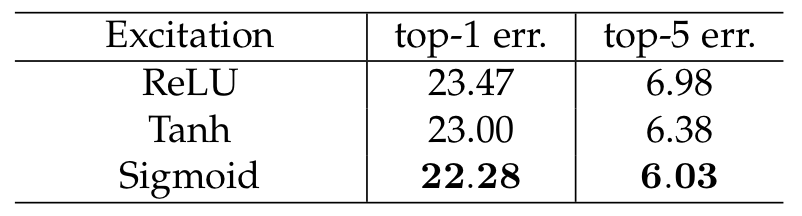
image.png

  • Excitation 연산 과정에서 두번째 FC 통과 이후 활성화 함수를 결정하는 실험이다. 논문 설명 과정에서 갑자기 왠 Sigmoid? 라는 의문이 들었을 텐데 이게 가장 성능이 잘 나왔다고 한다.

Role of Excitation

  • 추가적으로 Excitation이 정확히 어떻게 성능을 개선시켜주는지에 대한 실험을 진행하였다.
  • 각 스테이지 별 activation 값을 그래프로 표현해보았다.

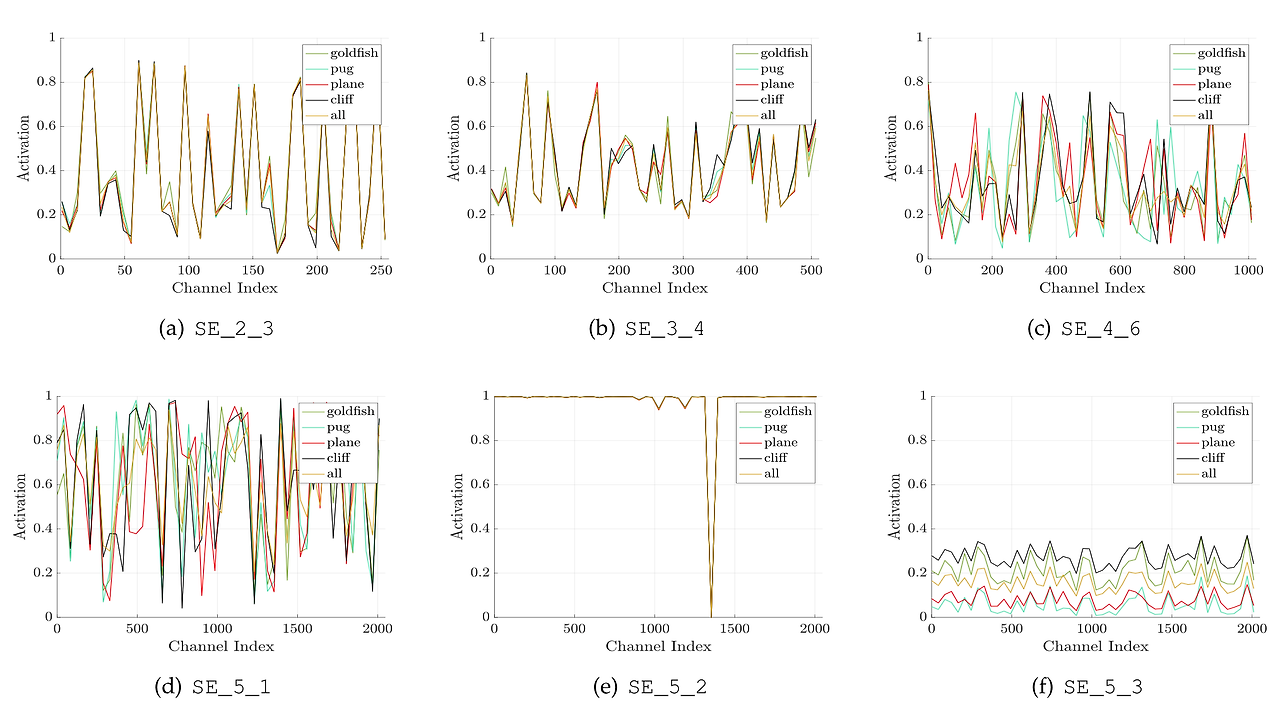
image.png

  • 초반 그래프를 보면 클래스와 관계 없이 그래프가 모두 비슷한 걸 볼 수 있는데 네트워크 초기에는 Feature가 클래스 별로 아직 구분이 덜 되는 것을 보여준다.
  • 이후 SE_4_6 그리고 SE_5_1을 보면 클래스 별로 그래프 양상이 많이 다른 것을 볼 수 있는데 이는 클래스 별로 특징을 잘 구별해낸 것을 알 수 있다.
  • 추가로 SE_5_2 그리고 SE_5_3은 후반임에도 불구하고 그래프 별 차이가 많이 없다. 실제로도 후반에 있는 SE를 제거했을 때 성능 차이가 크지 않았다고 한다.

SE Block의 위치

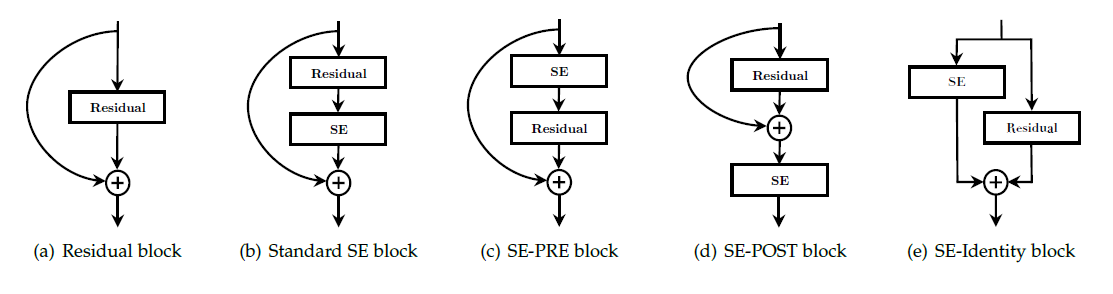
image.png

  • 논문에서는 SE Block의 위치를 바꿔보며 실험을 진행해보았다. (ResNet-SE인 상황)
  • 일단 위 그림만 봐도 (d)와 (e) 옵션은 구조 자체가 말이 안되는 것을 볼 수 있다.
    • (e) 같은 경우 ResNet의 identity mapping의 의의를 해치기 때문에 불가.
    • (d)는 일단 Full Pre-Act.를 기준으로 봤을 때 Full Pre-Act.의 의의를 해친다. Full Pre-Act.의 존재 의의는 identity mapping으로 넘어오는 정보들을 손실 없이 순전파 및 역전파 전달을 해주기 위함이다. 하지만 더해진 이후 SE를 통과시키면 정보의 변형이 일어나 손실된다.
  • 이후 (b)와 (c)를 실험해보았을 때 (b) 구조가 성능이 가장 잘 나왔다고 한다.

코드 구현

class SEBlock(nn.Module):
    def __init__(self, in_channels, r = 16):
        super().__init__()
        self.squeeze = nn.AdaptiveAvgPool2d((1,1))
        self.excitation = nn.Sequential(nn.Linear(in_channels, in_channels // r),
                                        nn.ReLU(inplace=True),
                                        nn.Linear(in_channels // r, in_channels),
                                        nn.Sigmoid())

    def forward(self, x):
        SE = self.squeeze(x)
        SE = SE.reshape(x.shape[0],x.shape[1]) # 개x채로 바꿔주기 위함
        SE = self.excitation(SE)
        SE = SE.unsqueeze(dim=2).unsqueeze(dim=3) # 개채11로 만들어주기 위함
        x = x * SE
        return x
  • 해당 논문은 네트워크 자체가 아니라 네트워크에 들어가는 블럭을 소개하는 논문이라 블럭을 다루는 클래스 코드로만 해도 충분하다.
  • 일단 위에서 설명했듯이 Squeeze는 GAP로 진행해준다.
  • 이후 Excitation은 Linear, ReLU, Linear, Sigmoid로 구현해준다. r값을 전달받아 채널을 축소 및 확장 하는 것을 알 수 있다.
  • 추가적으로 forward 메서드에서 reshape을 진행해주어 개x채 형태로 바꾸어준다.
    • 그 이유는 Linear가 개x채 형태로만 입력을 받기 때문이다.
  • 이후 unsqueeze로 원래 형태로 바꾼 이후 스칼라 곱을 해준 값을 리턴해준다.

Updated: