MobileNet V2

MobileNet V2 (2018.01)

등장 배경

해당 논문에서 언급하는 가장 큰 문제점은 ReLU의 정보 손실성이다.
ReLU란 Vanishing Gradient를 막는 차선책이지 최선책은 아니다. Linear Activation이라는 완벽한 해결책이 있지만 Non-Linearity 때문에 이를 사용하지 못하는 것이다.
이에 대해 MobileNet V2는 약간의 비선형성을 포기하고 정보의 손실을 막는 방식을 택하여 Inverted Bottleneck이라는 구조를 선보인다.
결국 MobileNet V2는 MobileNet V1보다 성능이 더 개선되고 파라미터 수도 더 줄어든 결과를 내놓는다.

논문 출처

1801.04381

ReLU의 문제점

ReLU는 $\max(0,x)$ 의 식을 갖는 활성화 함수이다.
ReLU가 처음 제시되었을 때 이는 입력 값이 양수 일때 반환하는 기울기가 1이기에 그라디언트가 손실 되는 문제를 어느정도 해결해주었다.
하지만 이는 그라디언트 손실 문제를 완벽히 해결하진 않았다. 입력 값이 음수이면 기울기가 0으로 정보를 없애기 때문이다.
물론 Linear Activation을 사용한다면 그라디언트 손실 문제따위 금방 해결되어버리지만 비선형성을 잃기에 사용되지 않았다.
이에 대한 문제점을 시각화하기 위해 논문에선 AutoEncoder 실험을 진행하였다.
- AutoEncoder란 입력 값을 받고 한 층의 레이어를 통과 후 입력 값과 똑같은 값을 출력해내는 것이다.
- 실험 결과 ReLU는 상당히 어려워하는 모습을 볼 수 있다.
- 물론 은닉 층의 노드 갯수를 늘리면 성능이 나아지는 모습을 보여주지만 Linear Activation이 사용되었으면 dim = 2면 충분히 바로 해결되는 문제이기에 ReLU의 정보 손실성을 강조해주는 실험 결과이다.
더군다나 MobileNet V2에선 ResNet의 구조를 사용하는데 Bottleneck 구조에선 채널 수가 줄어들기에 정보 손실이 더욱 막대할 것이다.

Inverted Bottleneck

위의 문제점을 해결하기 위해 논문에서 제시한 구조는 Inverted Bottleneck 구조이다.
Inverted라는 단어를 가지고 있듯 기존 Bottleneck 같이 채널 수를 줄이고 다시 늘리는 것이 아니라 채널 수를 늘리고 다시 줄이는 방식을 택한 것이다.
해당 방법이 가능했던 이유는 Depth-wise Separable Convolution으로 인해 대폭 줄인 파라미터 수 덕분이다.

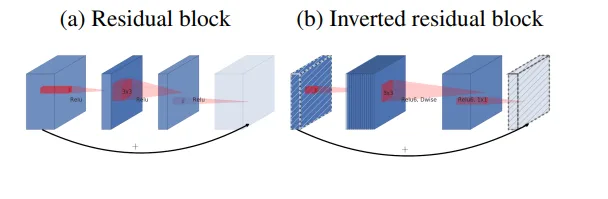
이에 대한 장점은 채널 수를 늘려 ReLU의 정보 손실량을 줄일 수 있다.
그렇다면 쭉 채널 수를 늘리면 되지 왜 다시 줄이는 방법을 택했을까?
- 물론 채널 수를 지속적으로 늘리면 파라미터 수가 기하급수적으로 증가할 것이다.
- 그리고 원래 채널 수로 돌아오면 skip-connection이 가능해진다.

정보 손실과 비선형성의 Trade-off (Linear Activation)

우선 Inverted Bottleneck의 연산 과정을 한번 알아보자.
- 입력 값이 들어오면 먼저 1x1 Convolution으로 채널 수를 늘려준다.
- ReLU6를 통과시킨 이후 3x3 Depth-wise Convolution으로 채널 별 spatial 정보를 추출한다.
- ReLU6를 통과시킨 이후 다시 1x1 Convolution으로 기존 채널 수로 줄여준다.
  - ReLU6란, 반환 값의 최대치를 6으로 제한시키는 것이다.
  - $\min(\max(0,x),6)$
  - 대부분의 모델이 activation 값이 6을 넘지 않아 6으로 제한시켜 계산에 사용되는 비트 수를 줄여 메모리 효율성을 늘리기 위함이다.
- Linear Activation을 통과시킨다.
Linear Activation이라니 참으로 황당한 연산 방식일 것이다. 요즘 논문에서 Linear Activation을 사용하는 것을 본지가 꽤나 오래됐을 것이다.
하지만 해당 논문에선 ReLU의 정보 손실성을 꽤나 강조하였고 채널을 줄인 이후 ReLU6를 통과시켜버리면 Inverted Bottleneck 구조의 의의를 무너뜨려버리는 셈이다.
즉, 약간의 비선형성을 포기하고 정보 손실을 줄이는 방식을 채택한 것이다.

전체 구조

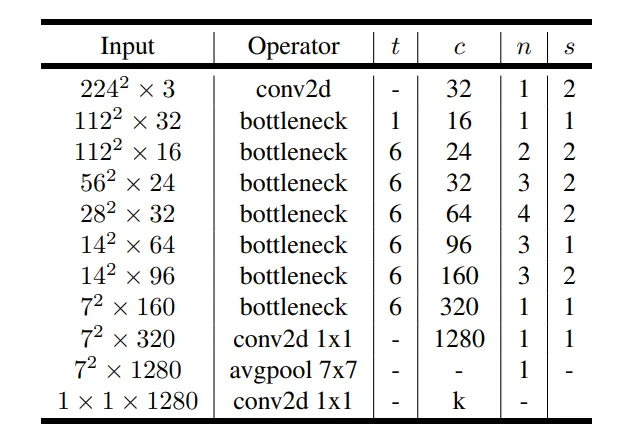
위 테이블에서 t는 expansion ratio 즉, inverted bottleneck에서 t배로 채널 수가 증가한다. c는 출력 채널수, n은 블럭 반복 횟수, s는 stride를 의미한다.
첫 Convolution은 기존 Convolution으로 진행되고 이후 첫 Bottleneck만 expansion없이 진행 후 GAP-FC 이전까지는 모두 t=6으로 inverted bottleneck으로 진행된다.
3번째 Convolution 과정을 보자면…
- 16 채널이 입력되어 채널이 6배 증가하여 96 채널이 된 이후 Depth-wise Convolution 진행이 된다.
- 이후 Point-wise Convolution으로 채널 수를 24로 줄인다.
- n = 2이기 때문에 한번 더 반복하는데 이번엔 입력 채널이 24이므로 채널이 144로 증가한다.
- 이후 Depth-wise Convolution 진행 후 Point-wise Convolution으로 24채널로 다시 복귀한다.
- 이때는 Skip-Connection이 성립이 된다. (입/출력 채널 수가 동일하기 때문이다)

성능 검증

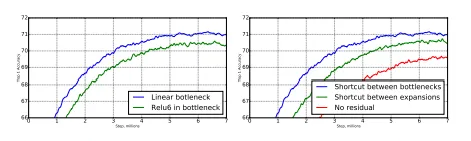
왼쪽 그래프를 보면 Inverted Bottleneck 마지막에 ReLU가 아닌 Linear Activation을 쓴 것이 성능이 확실히 더 개선된 것을 볼 수 있다.
또한, Skip-Connection의 구조도 Bottleneck 전체를 건너뛰는 구조가 성능이 가장 잘 나온 것을 볼 수 있다.

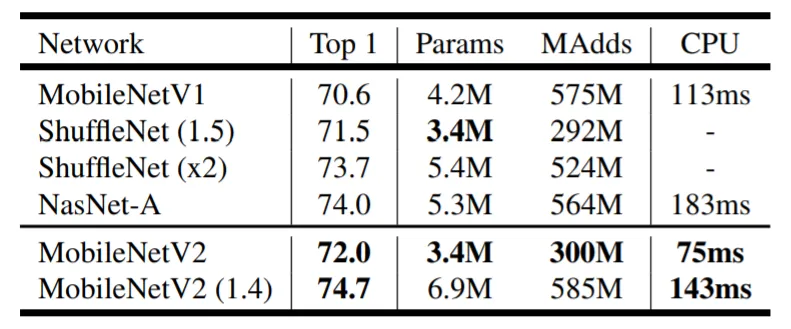
MobileNet V1과 비교하니 약 80만개의 파라미터 수를 줄이면서도 성능이 1.4% 개선된 것을 볼 수있다.

코드 구현

DepSepConv 클래스

  class DepSepConv(nn.Module):
      def __init__(self, in_channels, out_channels, stride):
          super().__init__()
    
          self.depthwise = nn.Sequential(nn.Conv2d(in_channels,in_channels,3, stride = stride, padding = 1, groups = in_channels, bias=False),
                                         nn.BatchNorm2d(in_channels),
                                         nn.ReLU6(inplace=True))
    
          self.pointwise = nn.Sequential(nn.Conv2d(in_channels,out_channels,1, bias=False),
                                         nn.BatchNorm2d(out_channels))
                                         # no activation!!
      def forward(self, x):
          x = self.depthwise(x)
          x = self.pointwise(x)
          return x

V1과 달라진 점은 Point-wise Convolution 연산에서 activation 파트가 사라졌다.

InvertedBlock 클래스

  class InvertedBlock(nn.Module):
      def __init__(self, in_channels, exp_channels, out_channels, stride):
          super().__init__()
    
          self.use_skip_connect = (stride==1 and in_channels==out_channels)
    
          layers = []
          if in_channels != exp_channels: # 채널 안늘어날 때는 1x1 생략. 즉, 1x1은 채널을 키워야할 때만 존재한다.
              layers += [nn.Sequential(nn.Conv2d(in_channels, exp_channels, 1, bias=False),
                                       nn.BatchNorm2d(exp_channels),
                                       nn.ReLU6(inplace=True))]
          layers += [DepSepConv(exp_channels, out_channels, stride=stride)]
    
          self.residual = nn.Sequential(*layers)
    
      def forward(self, x):
          if self.use_skip_connect:
              return x + self.residual(x) # 더하고도 ReLU 하지 않는다! 그래야 linear block이 되는 거니까 (근데 그냥 pre-act 구조로 쓴다면 어땠을까?는 약간의 아쉬움)
          else:
              return self.residual(x)

use_skip_connect라는 어트리뷰트를 만들어 stride가 1이고 입/출력 채널 수가 동일할 때만 skip-connection이 이루어지도록 해준다.
- forward 메서드 참고
t = 1 같이 채널 증가가 없을 때에는 if문으로 키우는 레이어를 생략시킨다.

MobileNetV2 클래스

  class MobileNetV2(nn.Module):
      def __init__(self, num_classes=1000):
          super().__init__()
    
          self.configs=[# t, c, n, s
                        [1, 16, 1, 1],
                        [6, 24, 2, 2],
                        [6, 32, 3, 2],
                        [6, 64, 4, 2],
                        [6, 96, 3, 1],
                        [6, 160, 3, 2],
                        [6, 320, 1, 1]]
    
          self.stem_conv = nn.Sequential(nn.Conv2d(3, 32, 3, padding=1, stride=2, bias=False),
                                         nn.BatchNorm2d(32),
                                         nn.ReLU6(inplace=True))
    
          in_channels = 32
          layers = []
          for t, c, n, s in self.configs:
              for i in range(n):
                  stride = s if i == 0 else 1
                  exp_channels = in_channels * t
                  layers += [InvertedBlock(in_channels=in_channels, exp_channels=exp_channels, out_channels=c, stride=stride)]
                  in_channels = c
    
          self.layers = nn.Sequential(*layers)
    
          self.last_conv = nn.Sequential(nn.Conv2d(in_channels, 1280, 1, bias=False),
                                         nn.BatchNorm2d(1280),
                                         nn.ReLU6(inplace=True))
    
          self.avg_pool = nn.AdaptiveAvgPool2d((1,1))
    
          self.classifier = nn.Sequential(nn.Dropout(0.2), # 논문에는 상세히 나와있진 않지만 토치 문서에 있어서 포함 -> 채널 축으로 특징들이 놓여있고 그것들을 일부 가려보며 학습하는 의미
                                          nn.Linear(1280, num_classes))
    
      def forward(self, x):
          x = self.stem_conv(x)
          x = self.layers(x)
          x = self.last_conv(x)
          x = self.avg_pool(x)
          x = torch.flatten(x, 1)
          x = self.classifier(x)
          return x