EfficientNet (2019.05)

등장 배경

  • MobileNet 출시 이후로 임베디드 환경에서도 활용될 수 있도록 파라미터 수와 레이턴시를 대폭 줄이며 성능을 유지하려는 실험이 많이 진행되었고 그에 대해 새로운 방법론을 제시한 것이 EfficientNet이다.
  • 대표적으로 Depth를 이용하여 성능을 개선하려 했던 VGGNet, ResNet, Width를 넓혔던 WideResNet, 그리고 많은 시도는 없었지만 Resolution을 조정하였던 MobileNet이 있다.
  • EfficientNet은 성능을 좌지우지 하는 세가지 요소 (Depth, Width, Resolution)을 한번에 조절하여 최대의 효율에서 최대의 성능을 내려고 하였다.

논문 출처

1905.11946

Compound Scaling

  • EfficientNet은 세가지 모두 키우자는 의견을 제시했고 여기서 가장 중요한 점은 효율적으로 키우는데에 집중한 것이다.

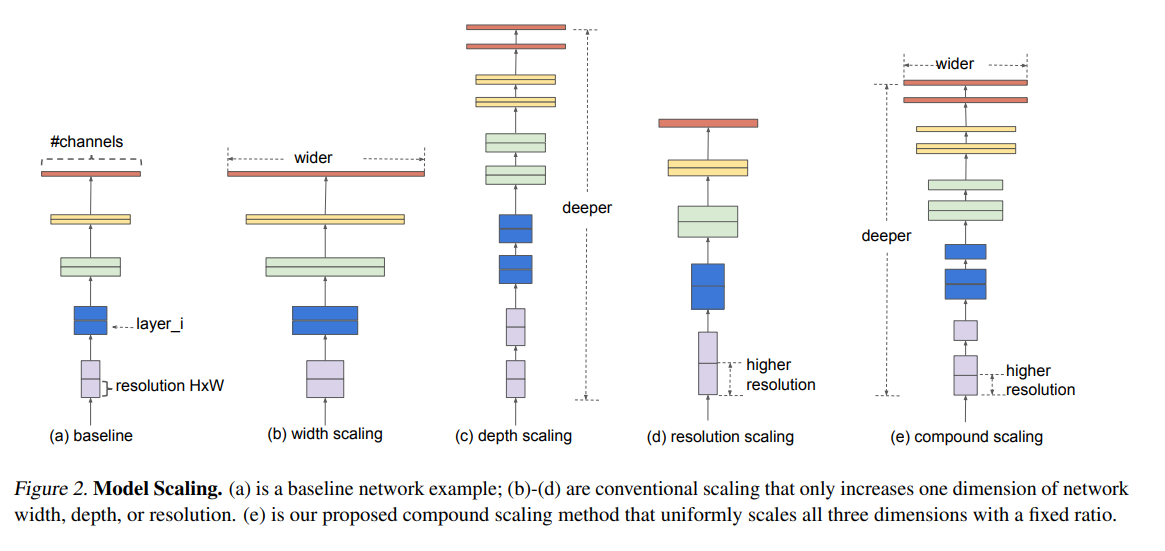
image 17.png

  • (e) 부분이 세가지 요소를 모두 키운 그림이다.

왜 세가지 모두 키워야 되는 걸까?

  • 예를 들어 Resolution을 키운다고 가정해보자.
    • Resolution이 커지면 그만큼 디테일하게 잡을 요소들이 많아질 것이고 이는 채널 수를 늘려 특징 수를 늘려야한다.
    • 또한 Resolution이 커지면 그에 따라 Receptive Field도 커져야 하기에 Depth도 커져야 된다.
  • 또한 세가지 중 두가지를 고정시켜놓고 한가지만 키웠을 때의 성능 그래프를 보면 이해가 간다.

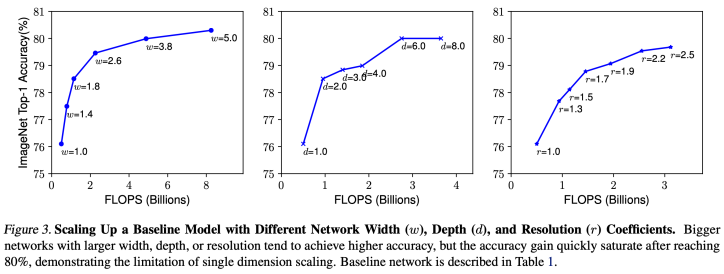
image.png

  • 세가지 요소 모두 증가할수록 성능도 같이 증가되는 것을 볼 수 있다.
    • 하지만 depth 같은 경우 빠르게 saturate 되는 것을 볼 수 있고 resolution 또한 그렇다.

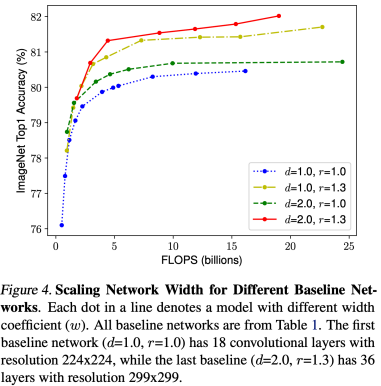
image.png

  • 또한 왼쪽의 그래프를 보자. FLOPS = 10 이라는 선을 그려놓고 각 선의 성능을 비교해보자.

  • 같은 연산량 기준 d, r 변화 없이 w만 키운 것이 성능이 가장 낮고 빨간 선이 가장 성능이 좋다.

  • 네 개의 선 모두 d,r,w의 수치가 다른데 이는 무엇을 말하냐면 같은 연산량에서 최적의 성능을 내는 d,r,w의 조합이 있다는 것을 뜻한다.

밸런스 맞추기

  • 그렇다면 최적의 성능을 내는 d,r,w는 어떻게 찾나?
  • 논문에서는 다음과 같은 식을 제시했다.
    • $d = \alpha^\phi, \enspace w = \beta^\phi,\enspace r = \gamma^\phi$
  • 여기서 $\alpha,\beta,\gamma$는 유지한 상태로 $\phi$를 변경하며 연산량을 늘리자고 말한다.
  • 또한, $\alpha\beta^2\gamma^2 \approx2$ 로 설정하여 연산량은 $2^\phi$가 되도록 하였다.
    • 여기서 왜 $\beta$와 $\gamma$는 제곱을 해주었나?
    • $\gamma$는 resolution을 뜻하는데 resolution은 width x height 이기 때문에 제곱으로 연산량이 늘어난다. $\beta$는 width이고 입/출력 채널 수 둘 다 늘어나기에 제곱으로 연산량이 늘어난다.
  • 그러면 $\alpha\beta^2\gamma^2 \approx2$를 충족하는 최적의 $\alpha,\beta,\gamma$는 무엇인가?
    • $\alpha=1.2, \enspace \beta = 1.1, \enspace \gamma = 1.15$
    • 해당 값은 exhausted search 즉 노가다를 통해 성능이 가장 좋은 값을 찾았다고 한다.

EfficientNet B0 ~ B7

  • EfficientNet은 리소스 사용량에 따라서 B0 부터 B7 까지 나뉜다.
  • B0은 Baseline 모델로써 d, r, w가 1일 때의 모델을 뜻하고 B7으로 갈 수록 $\phi$가 커지면서 d,w,r이 커진다.

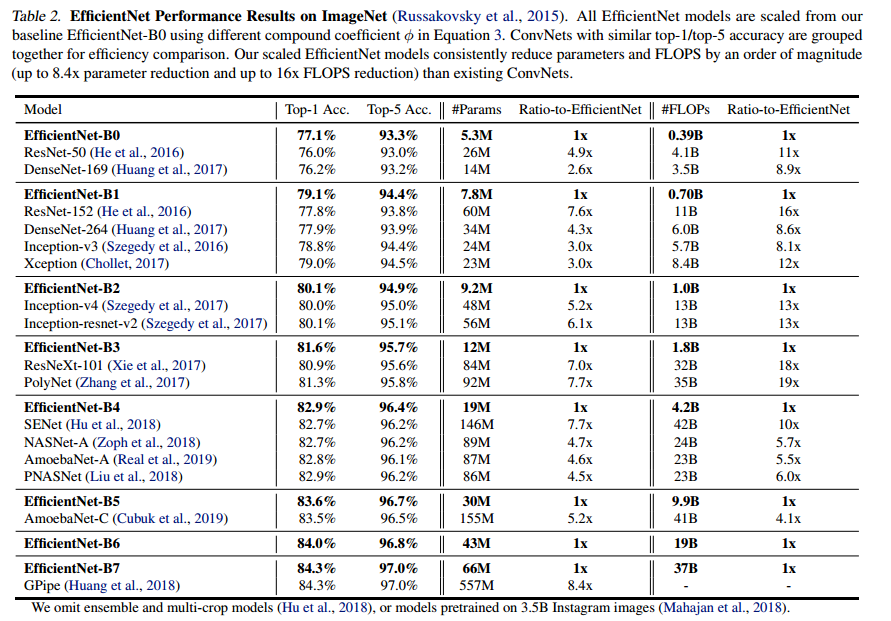
image.png

  • 각 버전 별로 성능이 비슷한 모델과 비교하여 테이블로 정리하였다.
  • B3 같은 경우 동일 성능 대비 연산량이 약 20배가 차이 날 정도로 큰 격차를 보여주었고 성능이 가장 뛰어난 B7 같은 경우는 동일 성능 대비 8배 이상 파라미터 수를 줄였다.

전체 구조

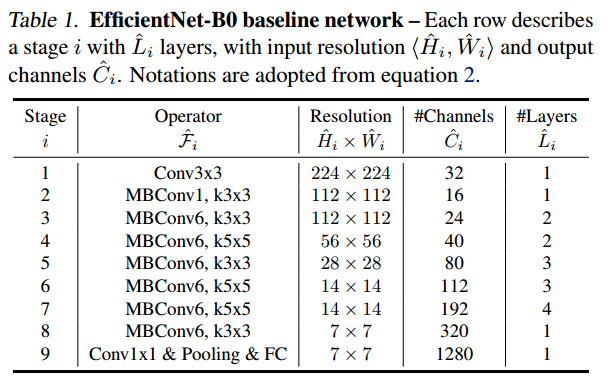
image.png

  • 이 구조 또한 NAS를 통해 찾은 구조이며 전체적인 틀은 MobileNetV3와 다를 것이 없다.
    • Depth-wise Separable Convolution을 사용하며
    • Skip-connection도 도입되있으며
    • SE가 추가되었고
    • Inverted Bottleneck이 도입된 블럭이 MBConv이다.
  • B7으로 갈수록 $\phi$가 커지면 그에 맞게 Resolution, Channel, Layers가 커진다.

Stochastic Depth

  • EfficientNet은 훈련 과정 중에 stochastic depth라는 기술을 도입했다.
  • CNN의 dropout이라고 보면 되는데 MLP에선 드롭 아웃이 노드를 지우는 것이었지만 stochastic depth는 블럭의 출력을 일정 확률로 0으로 만들어 블럭 자체를 없다고 가정해버리는 것이다.
    • 참고로 skip-connection이 있는 곳만 stochastic depth를 적용해야한다.
    • 출력을 0 자체로 바꿔버리기에 identity mapping이 없으면 그 이후 모든 출력이 0으로 바뀐다.
  • 또한 파이토치에서의 dropout과 stochasic depth의 구현은 좀 특이하다.
    • 훈련 과정에선 일정 확률로 인해 드롭되지 않은 블럭의 출력에는 1/(1-p)가 곱해져서 나오게 된다.
    • 해당 이유는 원래였으면 다른 노드의 값까지 합쳐져 출력이 나와야 되는데 드롭이 되면 크기 차이가 존재하기에 1/(1-p)를 곱해주어 차이를 상쇄시키는 것이다.
  • 드롭아웃과 마찬가지로 시험단계에서는 쓰이지 않는다.

성능 검증

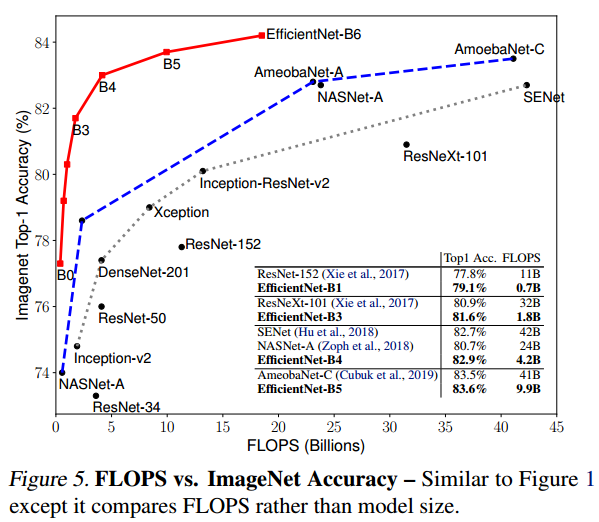
image.png

  • EfficientNet이 왼쪽 위 코너에 몰려있는 것을보아 동일 연산량 대비 정확도가 다른 모델에 비해 상당히 높다는 것을 알수 있고 효율의 극치를 구현한 모델이라는 것을 알 수 있다.

Updated: