DenseNet

DenseNet (2016.08)

등장 배경

ResNet의 skip-connection이 등장하면서 해당 구조에 대한 연구가 끊임없이 이어져왔다.
물론 ResNet이 엄청난 성능을 보여주었지만 skip-connection 구조에 대한 단점은 존재했다. Skip-Connection은 기존 입력 값을 더해주는 행위 (identity mapping)이 이루어지는데 더해줌으로써 정보에 대한 손실이 일어난다.
- 예를 들어 출력 값이 5.1이면 이게 5+0.1인지, 5.2-0.1인지 알 수가 없다.
또한 skip-connection도 vanishing gradient 문제를 해결하진 못하였다.
이에 대한 해결책으로 해당 논문의 저자가 내놓은 것이 Dense Connection 이며 해당 구조는 여태 있던 모든 입력 값을 concatenate 하여 입력으로 넣는다.
해당 모델은 ILSVRC 2016에서 2등을 차지하였다.

논문 출처

1608.06993

Dense Connection

먼저 기존 Convolution 연산을 식으로 세워보자.
- $x_l = H(x_{l-1})$
- 여기서 $H(x)$는 BN, ReLU, Conv. 를 내포하고 있는 composite function이다.
- Full Pre-Activation 구조를 사용하여 BN ⇒ ReLU ⇒ Convolution 순으로 연산이 진행된다.
Skip-Connection이 첨가된 식은 이러하다.
- $x_l = H(x_{l-1})+x_{l-1}$
Dense Connection은 이러하다.
- $x_l = H([x_0, x_1,x_2, \cdots ,x_{l-1}])$
- $l$번째 레이어에서는 $l-1$까지의 모든 입력 값을 depth 방향으로 concat 한 것을 입력 값으로 받아들인다.

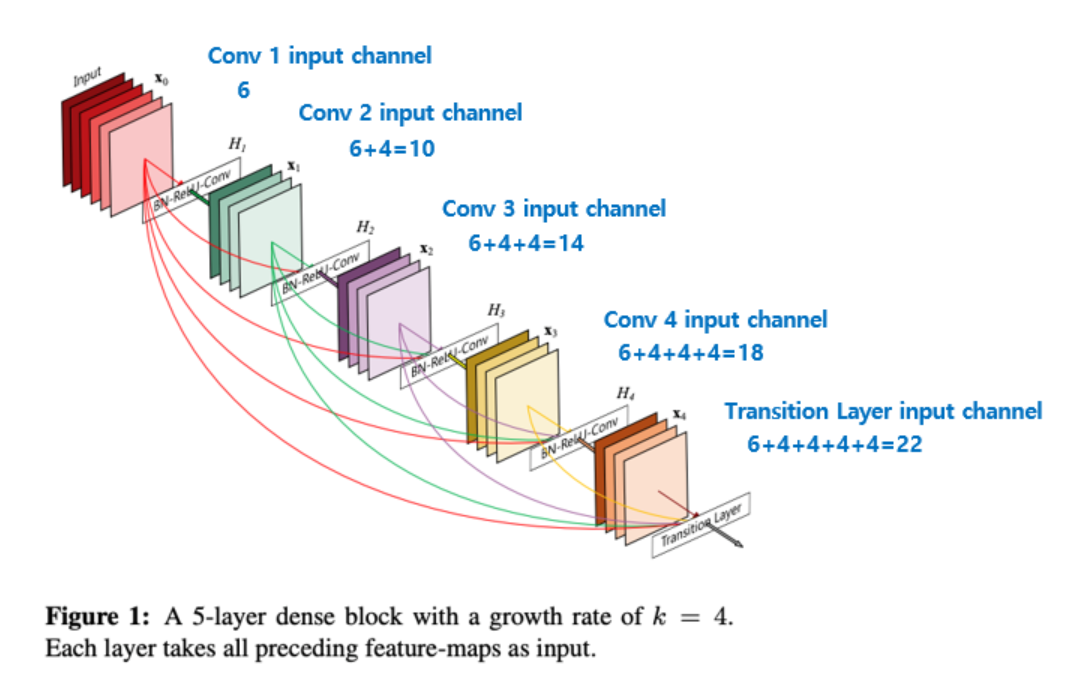
image 18.png

Growth Rate란?
- 위의 그림에선 예시로 growth rate k = 4로 설정하고 있다.
- k 값은 각 dense 층 마다의 출력 채널 값을 의미한다. 그리고 Dense Connection의 특성 상 한개의 레이어를 통과할 때 마다 concat 되기 때문에 k만큼 입력 채널 수가 늘어날 것이다.

DenseNet의 Bottleneck 구조

위의 Dense Connection을 보면 의문점이 하나 들 것이다.
점점 입력 값의 채널 수가 늘어나고 출력 채널 수가 k로 고정이 되면 Dense Block의 깊이가 깊어질수록 Bottleneck이 심해질 것이다.
- 당장 위의 예시만 봐도 마지막에선 22채널에서 4채널로 급격하게 채널 수가 줄어든다.
해당 현상을 완화시키기 위해 DenseNet도 Bottleneck 구조를 도입하였다.
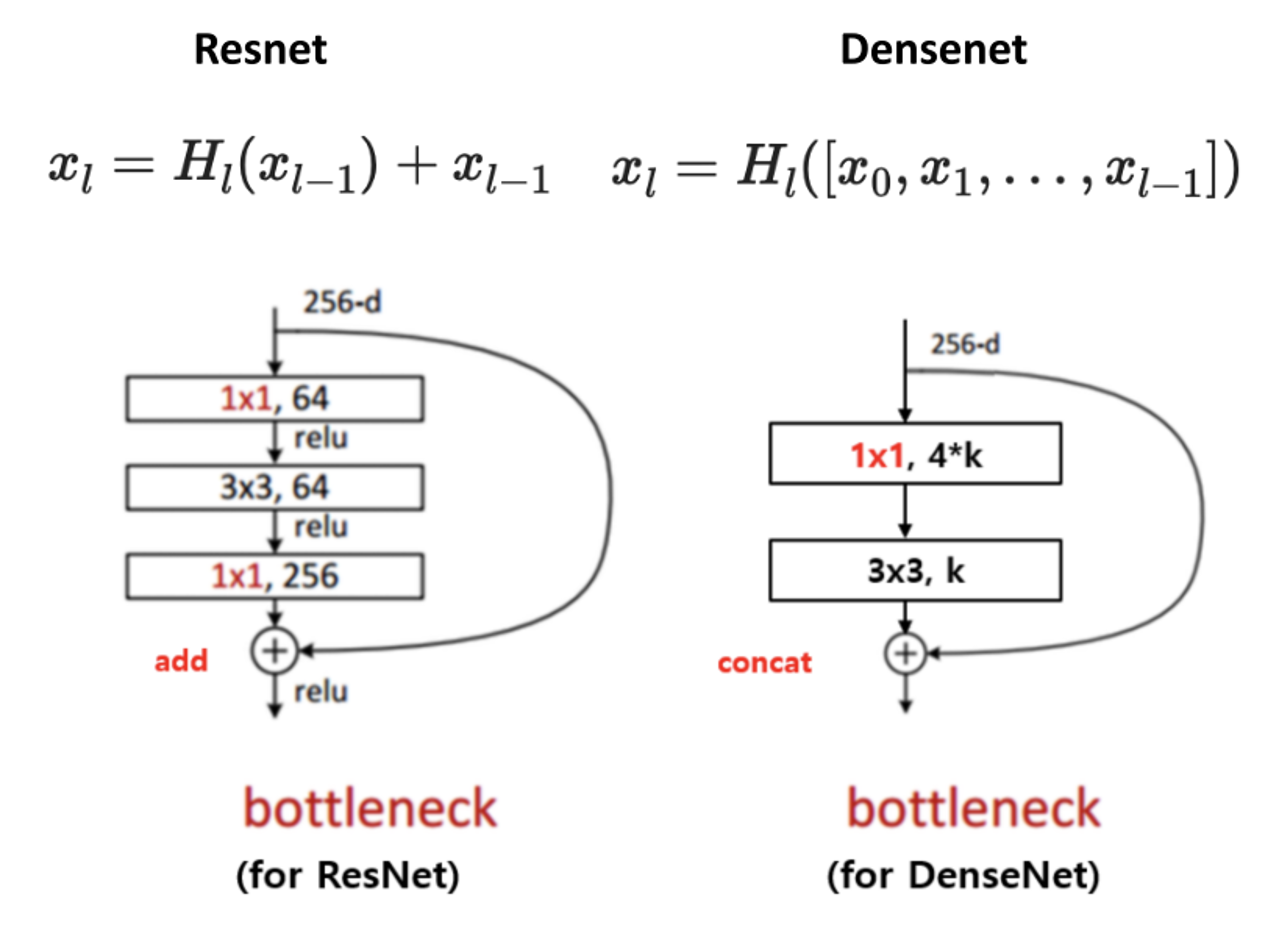
- 위 그림의 오른쪽 구조를 보면 입력 값이 들어왔을 때 1x1 Conv.로 채널 수를 먼저 4k로 줄여준다. (혹은 초반 단계에는 채널 수가 늘어날 것이다.)
- 이후 3x3 Conv.로 k 채널로 줄여주며 점진적으로 채널 수를 줄여준다.
- 예를 들어 입력 채널이 20이고 k=4라면, 20 채널에서 16 채널로 줄인 다음 4 채널로 줄이고 처음 입력이었던 20 채널과 concat. 되어 24 채널의 출력 값이 나오는 것이다.
- 참고로 위 그림에 블록에는 BN ⇒ ReLU ⇒ Conv. 가 다 포함되어 있는 상태이다.

Transition Layer

Dense Connection의 특성 상 concatenate을 해야되기 때문에 피처 맵의 사이즈는 동일해야 될 것이다.
하지만 CNN의 특성 상 피처 맵의 사이즈는 풀링 혹은 stride를 통해 사이즈를 줄여나가야 된다.
이러한 과정을 넣기 위해 Dense Connection은 Dense Block이라는 개념으로 구분해놓고 Dense Block들 사이에 Transition Layer를 도입하였다.

위 그림과 같이 블록들 사이에 Conv.와 Pooling이 포함되어 있는데 이를 Transition Layer로 일컫는다.
- Conv.는 1x1로 채널 수를 반으로 줄여준다.
- Pooling은 2x2 Avg. Pooling으로 사이즈를 반으로 줄여준다.

전체적인 구조

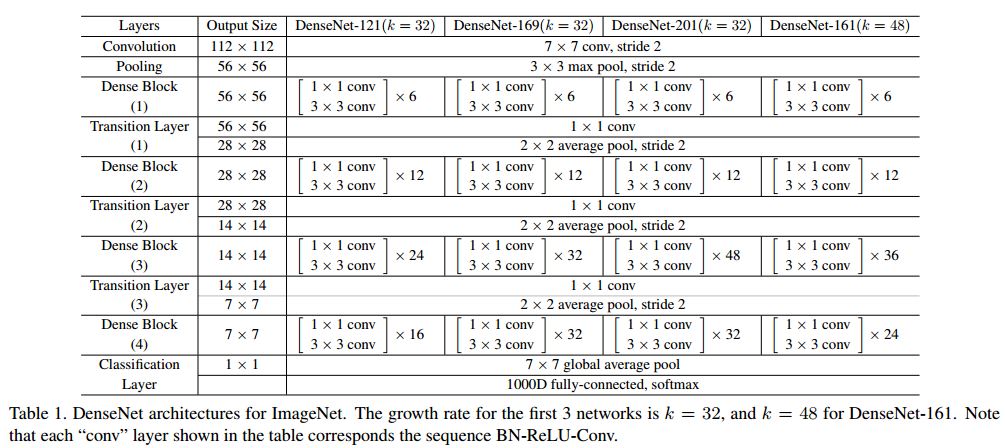
성능 검증

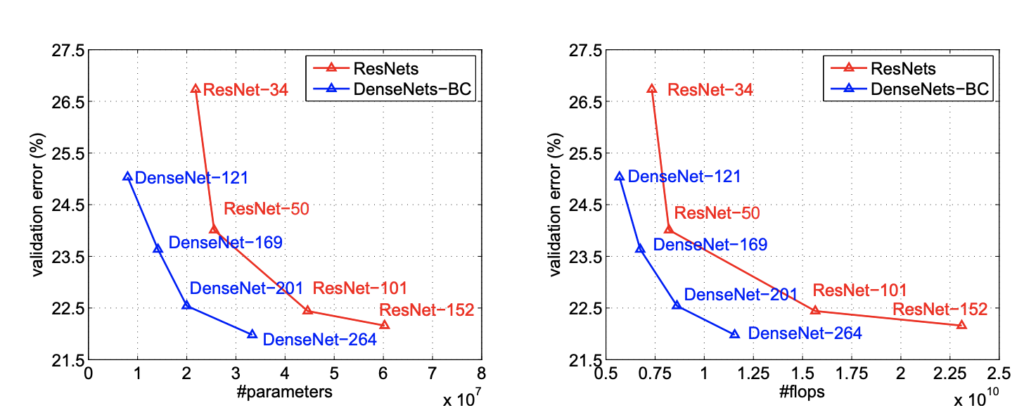
ResNet과 비교하여 동일 수의 파라미터일 때 성능이 훨씬 좋은 것을 볼 수 있다.

코드 구현

Bottleneck Class

  class Bottleneck(nn.Module):
      def __init__(self, in_channels, k):
          super().__init__()
    
          self.residual = nn.Sequential(nn.BatchNorm2d(in_channels),
                                        nn.ReLU(inplace=True),
                                        nn.Conv2d(in_channels, 4*k, kernel_size=1, bias=False),
                                        nn.BatchNorm2d(4*k),
                                        nn.ReLU(inplace=True),
                                        nn.Conv2d(4*k, k, kernel_size=3, padding=1, bias=False))
    
      def forward(self, x):
          return torch.cat([x, self.residual(x)], 1) # x가 바로 직전 채널 뿐만 아니라 그 전것도 모두 가지고 있음

위에서 설명했듯이 1x1 Conv.를 이용해 4k 채널로 증가 혹은 감소 시킨 뒤 3x3 Conv.를 이용하여 k개의 채널로 줄인다.
Full Pre-Activation 구조를 따라 BN ⇒ ReLU ⇒ Conv. 순으로 코드가 작성된 것을 볼 수 있다.
또한 출력 값이 Concat 그 자체 이기때문에 굳이 이전 블럭의 입력 값을 따로 저장할 필요없이 Concat. 출력 값을 계속 넘겨줌으로써 Dense Connection을 구현하였다.

Transition Class

  class Transition(nn.Module):
      def __init__(self, in_channels, out_channels):
          super().__init__()
    
          self.transition = nn.Sequential(nn.BatchNorm2d(in_channels),
                                          nn.ReLU(inplace=True),
                                          nn.Conv2d(in_channels, out_channels, 1, bias=False),
                                          nn.AvgPool2d(2))
    
      def forward(self, x):
          return self.transition(x)

Transition Layer를 담당하는 클래스 코드이다.
이 또한 Full Pre-Act. 구조를 따라 BN ⇒ ReLU ⇒ Conv. 순으로 1x1 Convolution이 적용되어 채널 수를 조정한다.
이후 Avg. Pooling을 통해 사이즈를 반으로 줄여준다.

DenseNet Class

  def make_dense_block(self, in_channels, nblocks):
          dense_block = []
          for _ in range(nblocks):
              dense_block += [ Bottleneck(in_channels, self.k) ]
              in_channels += self.k
          return nn.Sequential(*dense_block)

우선 먼저 DenseNet 클래스 메서드 함수인 make_dense_block을 살펴보자.
해당 메서드는 DenseBlock을 생성하는 함수로써 Bottleneck 인스턴스를 생성하고 in_channels += self.k 코드를 통해 한개의 Bottleneck을 지날때마다 concat 된 채널 수를 업데이트 해준다.

  def __init__(self, num_block_list, growth_rate, reduction=0.5, num_class=1000):
          super().__init__()
          self.k = growth_rate
    
          inner_channels = 2 * self.k
    
          self.conv1 = nn.Sequential(nn.Conv2d(3, inner_channels, kernel_size=7, stride=2, padding=3, bias=False),
                                     nn.BatchNorm2d(inner_channels),
                                     nn.ReLU(inplace=True),
                                     nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
    
          layers = []
          for num_blocks in num_block_list[:-1]:
              layers += [self.make_dense_block(inner_channels, num_blocks)]
              inner_channels +=  num_blocks * self.k
    
              out_channels = int(reduction * inner_channels)
              layers += [Transition(inner_channels, out_channels)]
              inner_channels = out_channels
    
          layers += [self.make_dense_block(inner_channels, num_block_list[-1])]
          inner_channels += num_block_list[-1] * self.k
    
          layers += [nn.BatchNorm2d(inner_channels)]
          layers += [nn.ReLU(inplace=True)]
          self.features = nn.Sequential(*layers)
          self.avgpool = nn.AdaptiveAvgPool2d((1, 1))
          self.linear = nn.Linear(inner_channels, num_class)
    
          # Official init from torch repo.
          for m in self.modules():
              if isinstance(m, nn.Conv2d):
                  nn.init.kaiming_normal_(m.weight)
              elif isinstance(m, nn.Linear):
                  nn.init.constant_(m.bias, 0)

init 메서드를 살펴보자면 우선 growth rate와 reduction ratio를 전달 받는다.
- 여기서 reduction ratio는 transition 단계에서 얼마나 사이즈와 채널을 줄일지에 대한 하이퍼 파라미터 이고 보통 0.5를 사용한다.
Full Pre-Act. 구조를 따라 일단 첫번째 Conv. 블럭은 7x7로 시작하고 본래 순서인 Conv. ⇒ BN ⇒ ReLU를 따라간다.
그리고 채널 수는 논문에 명시된대로 2k로 채널을 늘려준다.
이후 마지막 스테이지 전까지만 for loop을 통해 구조를 만들어준다.
- 마지막 스테이지는 Dense Block 이후 Transition Layer가 아니라 GAP-FC가 따라오기 때문에 For Loop에서 제외된다.
또한, Dense Block을 통과할때마다 채널수가 달라지기에 inner_channels += num_blocks * self.k 코드를 통해 채널 수를 업데이트 해준다.
마지막으로 GAP-FC를 layers 리스트에 추가해주고 weight initialization 코드를 작성해주면 코드 구현은 끝난다.