ResNet

ResNet(2015.12)

요약

ResNet은 Vanishing Gradient 문제를 해결하기 위해 Skip-Connection을 도입한 모델로, 깊은 네트워크에서도 성능 저하를 방지하며, Bottleneck 구조를 통해 파라미터 수를 줄인다. ResNet은 VGGNet과 비교해 훨씬 더 깊은 네트워크를 가능하게 한다.

논문 출처

1512.03385

기존 문제점

한창 Vanishing Gradient 문제가 대두되자 그에 대한 해결 방안으로 Batch Normalization과 ReLU가 도입되었다.
BN과 ReLU의 조합으로 문제가 해결된듯 하였으나 Kaiming He는 새로운 문제를 제기하였다.

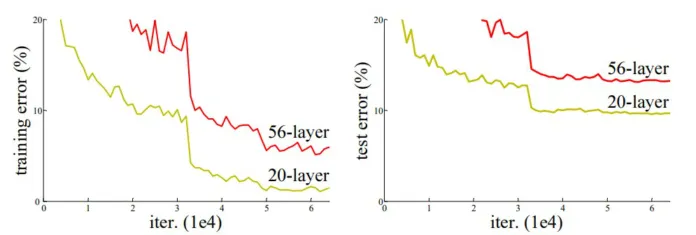
image 9.png

Vanishing Gradient 문제가 해결이 됐으면 층이 깊어질수록 성능이 올라가는게 정상적인 문제일텐데 왜 층이 깊어지면 성능이 떨어질까?
예를 들어 50층짜리 모델이 10층짜리 모델의 성능을 흉내내고 싶다면 나머지 40층을 0으로 만들면 10층을 따라할 수 있을텐데 어째서 56층이 20층보다 성능이 안나오는 것인가?
- 위의 그림을 보면 56층의 에러가 20층의 모델의 에러보다 높은 것을 볼 수 있다.
- 하지만 이게 또 Vanishing Gradient문제는 아닌게 에포크가 지날수록 성능은 낮아지고 있기에 그라디언트가 손실되는 것 같지는 않다.
- 실제로 Kaiming He가 층마다 그라디언트 값을 확인해봤을 때 그라디언트가 손실되지는 않는다고 하였다.
그렇다면 Vanishing Gradient 말고 다른 문제가 있다는 결론에 다다르게 된다.

Loss Landscape (논문 외 주제)

위에서 대두된 새로운 문제를 논문상에서는 Degradation이라고 언급하지만 나중에 되서야 많은 이들이 Loss Landscape가 너무 복잡해지고 꼬불꼬불해지는 문제라는 것이 정설이다.

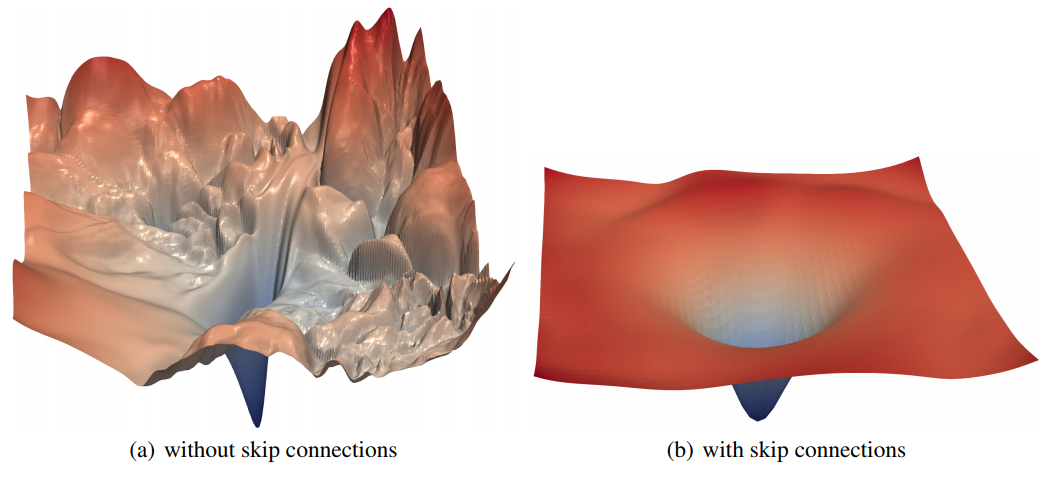
여기서 먼저 잠깐 언급하자면 ResNet은 skip-connection을 도입한 모델이다.
위의 그림은 ResNet을 도입한 Loss Landscape인데 skip-connection을 도입하자 loss landscape가 매끈해지고 local minimum에 빠질 위험이 줄어든다.
하지만 여기서 드는 고민이 있어야한다.
- Loss Landscape를 어떻게 3차원상에 그릴수가 있나?
- Weight의 수치에 따라 loss가 달라지는 것이면 모든 파라미터를 축으로 삼고 그려야된다. 그러면 고작 3차원으로 그릴 수가 없을텐데?
$\theta^* = \text{optimized weight vector} \ \delta_{i,j} = \text{scaled random vector of ith layer, jth filter} \ \eta_{i,j} = \text{another scaled random vector of ith layer, jth filter}$ 라고 가정했을 때,
$f(\alpha, \beta) = L(\theta^*+\alpha\delta_{i,j} + \beta\eta_{i,j})$ 함수를 그린 것이 Loss Landscape다.
- $\alpha$와 $\beta$를 -1과 1사이로 조정하며 그리는 것이다.

라고 말하면 이해가 잘 안될 거 같아서 조금 이해하기 쉽게 풀어 서술해보겠다.

$\theta^*$는 즉 학습이 되어진 파라미터 벡터이다. 해당 벡터의 위치를 중앙으로 두고 Local Minimum이라는 가정한다.
이후 $\theta^*$의 크기와 동일하게 $N(0,1)$ 에서 랜덤하게 벡터를 두개 만든다. (그게 $\delta, \eta)$
- 즉, $\delta, \eta$는 (1 x 모든 파라미터의 갯수) 사이즈가 된다.

그 다음 filter-wise normalization이라는 과정을 거쳐야된다. (필수는 아니고 옵션이지만 정규화를 진행하면 loss landscape가 더 잘 나온다고 한다.)

$\delta_{i,j} = \dfrac{\delta_{i,j}}{

\delta_{i,j}

_2}

\theta^*_{i,j}

_2$

델타 벡터를 델타 벡터의 크기로 나누어 크기를 1로 normalize를 해준 다음 최적화된 벡터의 크기를 곱해주는 것이다.

Skip-Connection / Residual Learning

위의 문제를 해결하기 위해 He가 제안한 방법은 Skip-Connection이다.

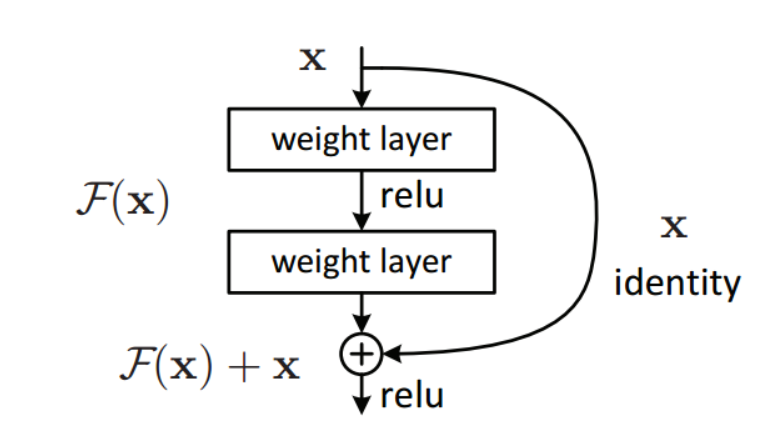
즉, 블럭을 통과하기 전의 값을 출력 값에 더해주는 것이 skip-connection이다.
그렇다면 왜 이러한 구조가 성능 개선에 도움이 되는 걸까?
$H(x)$가 optimal 한 블럭이라고 가정하자.
- 즉, 학습이 되어 Loss가 0이 되는 weight들이 H(x)인 것이다.
그리고 $H(x) = F(x)+x$인데 $H(x) = x$라는 구조로 만들고 싶다고 해보자.
그러면 $F(x)$가 0이 되도록 해야되는 것이다.
그런데 굳이 $F(x)+x$를 하여서 $H(x) = x$라는 형태로 만드는 이유가 무엇일까?
- Skip-connection이 없다면 weight layer들이 identity matrix가 되어야 입력 값이 그대로 나오는 반면,
- Skip-connection이 있다면 weight layer들이 다 0이면 출력값에 더해지는 x로 인해 출력값이 그대로 나오는 것이다.
- 그리고 weight initialization이 0 근처로 되기 때문에 $H(x) = x$로 만들기 더욱 쉬울 것이다.

왜 $H(x) = x$ 인가?

그런데 또 드는 의문점이 왜 $H(x) = x$인가? 이게 왜 성능이 올라가는가?

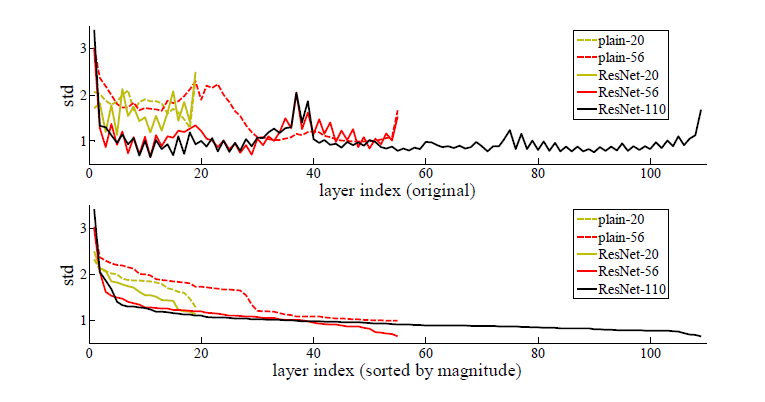
위의 그림은 각 레이어 사이의 편차 즉, standard deviation을 보여주는 그래프이다.
보면 층이 깊어질수록 std가 작아지는 것을 볼수가 있는데 이 말은 레이어에서 레이어로 넘어갈 때는 값이 차이가 크지 않다는 것이다.
즉, 차근차근 값을 바꾸어 나가는 것이 이상적인 모델이라는 결론에 다다른다. 그 말은 $H(x) \approx x$라는 뜻이다.
Skip-connection을 통해 x를 출력 값에 더해주면서 $H(x) \approx x$가 쉽게 학습되도록 유도하며 차근차근 값을 바꾸어 나가는게 좋은 모델이라는 것을 귀뜸 해준다는 것으로 이해하면 쉽다.

ResNet 구조

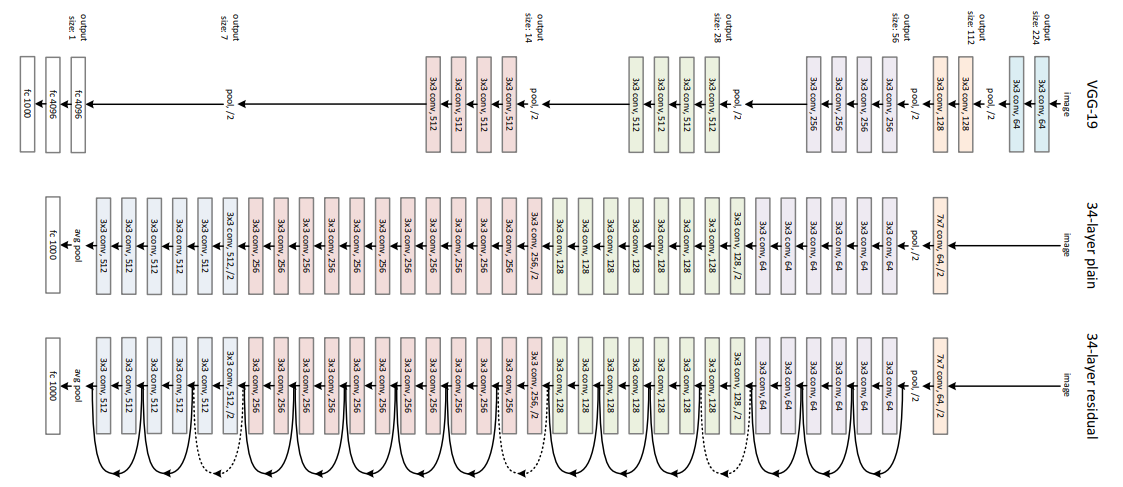
기본적으로 ResNet은 VGGNet의 구조를 따른다.
- 대부분 3x3 필터를 사용하며 피처맵의 사이즈를 반으로 줄일 때 채널 수를 늘린다.
- 대신에 사이즈를 줄일 때 풀링 대신 stride = 2를 사용을 한다.
Skip-Connection은 2층마다 매번 반복을 해준다.
- Conv → BN → ReLU → Conv → BN → +x → ReLU의 형식으로 반복이 된다.
점선은 채널 수가 바뀔 때마다 1x1 convolution을 통해 +x도 채널 수를 늘려준다는 의미이다.

Bottleneck

ResNet은 최대 152층을 가지는 모델이기에 아무리 가장 작은 3x3 필터를 사용하지만 파라미터 수가 너무나 많아진다.
그렇기에 He가 제안한 방법은 Bottleneck 구조이다.

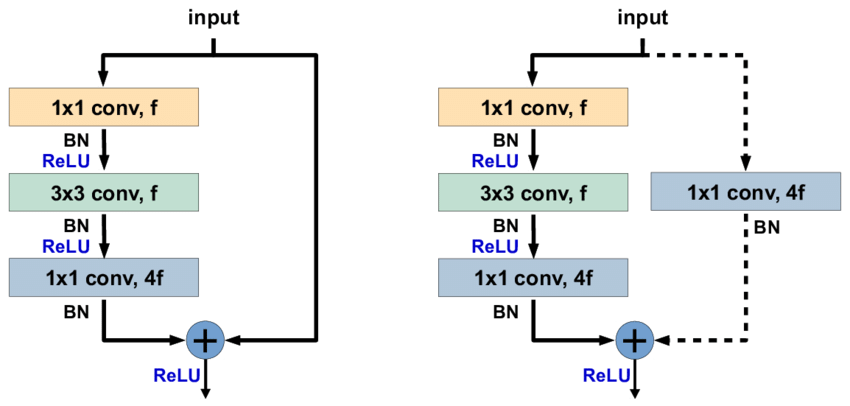
3x3블록 전후에 1x1블럭을 넣어줌으로써 디멘션을 줄여 파라미터 수를 줄이는 방법이다.
1x1 conv를 이용하여 채널 수를 반으로 줄여주며 계산 복잡성을 줄여준다.
이후 3x3 conv를 사용하여 1x1으로 인해 잃어버린 위치적 특성을 찾아주고
1x1로 다시 채널을 증가시켜주며 특징의 갯수를 늘려준다. (4f 즉, 4배로 늘려준다)
- 이전 층에서 stride = 2로 인해 피처 맵의 사이즈가 반으로 줄었으므로 최종적으로는 채널이 2배 늘어난 것과 동일하다.

Conclusion

ResNet은 Vanishing Gradient이외의 문제점을 발견하여 이를 해결한 최초의 모델이다.
- 물론 논문 내에서도 해당 문제에 대해 정확히 설명은 못했지만 해결은 하였다.
Skip-Connection의 등장으로 Inception과 VGGNet과 비교가 안될 정도로 층을 깊게 만드는데 성공하였다.

코드 구현

class BasicBlock(nn.Module):
    expansion = 1
    def __init__(self, in_channels, inner_channels, stride = 1, projection = None):
        super().__init__()

        #conv 레이어에서 bias=False인 이유는 BN에 bias가 들어가기 때문.
        self.residual = nn.Sequential(nn.Conv2d(in_channels, inner_channels, kernel_size = 3, stride = stride, padding = 1, bias = False),
                                      nn.BatchNorm2d(inner_channels),
                                      nn.ReLU(inplace = True),
                                      nn.Conv2d(inner_channels, inner_channels * self.expansion, kernel_size = 3, padding = 1, bias = False),
                                      nn.BatchNorm2d(inner_channels * self.expansion))
        self.projection = projection
        self.relu = nn.ReLU(inplace = True)

    def forward(self, x):
        residual = self.residual(x)

        if self.projection is not None:
            shortcut = self.projection(x) #점선 연결
        else:
            shortcut = x #실선 연결

        out = self.relu(residual + shortcut)

        return out

class Bottleneck(nn.Module):
    expansion = 4
    def __init__(self, in_channels, inner_channels, stride = 1, projection = None):
        super().__init__()

        self.residual = nn.Sequential(nn.Conv2d(in_channels, inner_channels, kernel_size = 1, bias = False),
                                      nn.BatchNorm2d(inner_channels),
                                      nn.ReLU(inplace = True),
                                      nn.Conv2d(inner_channels, inner_channels, kernel_size = 3, stride = stride, padding = 1, bias = False),
                                      nn.BatchNorm2d(inner_channels),
                                      nn.ReLU(inplace = True),
                                      nn.Conv2d(inner_channels, inner_channels * self.expansion, kernel_size = 1, bias = False),
                                      nn.BatchNorm2d(inner_channels * self.expansion))
        self.projection = projection
        self.relu = nn.ReLU(inplace = True)

    def forward(self, x):
        residual = self.residual(x)

        if self.projection is not None:
            shortcut = self.projection(x) #점선 연결
        else:
            shortcut = x #실선 연결

        out = self.relu(residual + shortcut)

        return out

class ResNet(nn.Module):
    def __init__(self, block, num_block_list, num_classes = 1000, zero_init_residual = True):
        super().__init__()
        
        self.in_channels = 64

        self.conv1 = nn.Conv2d(3, 64, kernel_size = 7, stride = 2, padding = 3, bias = False)
        self.bn1 = nn.BatchNorm2d(64)
        self.relu = nn.ReLU(inplace = True)
        self.maxpool = nn.MaxPool2d(kernel_size = 3, stride = 2, padding = 1)
        self.stage1 = self.make_stage(block, 64, num_block_list[0], stride = 1)
        self.stage2 = self.make_stage(block, 128, num_block_list[1], stride = 2)
        self.stage3 = self.make_stage(block, 256, num_block_list[2], stride = 2)
        self.stage4 = self.make_stage(block, 512, num_block_list[3], stride = 2)
        self.avgpool = nn.AdaptiveAvgPool2d((1,1))
        self.fc = nn.Linear(512 * block.expansion, num_classes)

        for m in self.modules():
            if isinstance(m, nn.Conv2d):
                nn.init.kaiming_normal_(m.weight, mode = 'fan_out', nonlinearity = 'relu')
        
        if zero_init_residual:
            for m in self.modules():
                if isinstance(m, block):
                    nn.init.constant_(m.residual[-1].weight, 0)
    
    def make_stage(self, block, inner_channels, num_blocks, stride = 1):
        if stride != 1 or self.in_channels != inner_channels * block.expansion:
            projection = nn.Sequential(nn.Conv2d(self.in_channels, inner_channels * block.expansion, kernel_size = 1, stride = stride, bias = False),
                                       nn.BatchNorm2d(inner_channels * block.expansion))
        else:
            projection = None
        
        layers = []
        layers += [block(self.in_channels, inner_channels, stride, projection)] # stride=2, 점선 연결은 첫 block에서만
        self.in_channels = inner_channels * block.expansion
        for _ in range(1, num_blocks): # 나머지 block은 실선 연결로 반복
            layers += [block(self.in_channels, inner_channels)]
        
        return nn.Sequential(*layers)
    
    def forward(self, x):
        x = self.conv1(x)
        x = self.bn1(x)
        x = self.relu(x)
        x = self.maxpool(x)

        x = self.stage1(x)
        x = self.stage2(x)
        x = self.stage3(x)
        x = self.stage4(x)

        x = self.avgpool(x)
        x = torch.flatten(x, 1)
        x = self.fc(x)

        return x