Vector & Matrix

1-3. 벡터와 행렬

열벡터

$\begin{bmatrix} 1 \ 2 \ 3 \ \vdots \end{bmatrix}$

행벡터

$\begin{bmatrix}1&2&3&\dots\end{bmatrix}$

행렬

$\begin{bmatrix}1 & 2& 3 \ 4&5&6\end{bmatrix}$

왜 사용하는가?

• 연립 방정식에서의 활용

$\begin{cases}x+2y = 4 \ 2x+5y = 9\end{cases}$$\implies \begin{bmatrix}1&2 \ 2&5\end{bmatrix}\begin{bmatrix}x \ y\end{bmatrix} = \begin{bmatrix}4 \ 9\end{bmatrix}$

→ 2개의 식에서 1개의 식으로 변환 가능

→ 더 확장하여 4개의 식도 1개의 식으로 변환이 가능하다.

$\begin{cases}x_1+2y_1 = 4 \ 2x_1+5y_1 = 9\end{cases} \(\And\begin{cases}x_2+2y_2 = 3 \\ 2x_2+5y_2 = 7 \end{cases}\) \implies \begin{bmatrix}1&2 \ 2&5 \end{bmatrix} \begin{bmatrix}x_1&x_2 \ y_1&y_2\end{bmatrix} = \begin{bmatrix}4 & 3 \ 9 & 7\end{bmatrix}$

→ 계수만 같으면 x,y의 열을 늘리며 확장이 가능

벡터의 크기와 방향

벡터의 크기와 방향이 같다면 같은 벡터라고 취급한다.

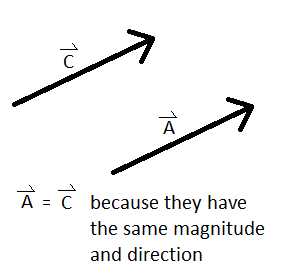
→ Norm = 벡터의 크기 = 길이

• $l2\enspace norm = \sqrt{x^2+y^2}$
• $l1\enspace norm = \midx\mid + \midy\mid$