Uniform and Normal Distribution

1-19. 균등 분포와 정규 분포

균등 분포(Uniform Distribution)

PMF

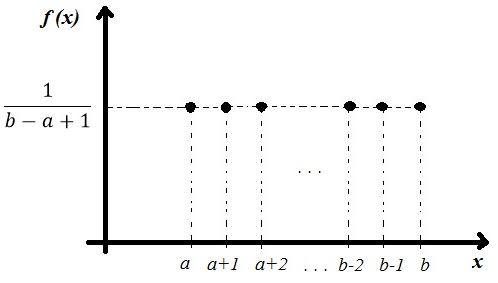
$image 5.png$

PDF

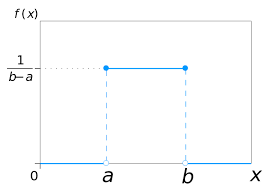
$image.png$

$\implies p(x) = \begin{cases}\frac{1}{b-a} \enspace \text{for a }\leq x \leq \enspace b \ 0 \enspace \text{otherwise}\end{cases}, \enspace X \sim U(a,b)$

$\implies \mu = \dfrac{(a+b)}{2}, \enspace \sigma^2 = \dfrac{(b-a)^2}{12}$

정규 분포(Normal / Gaussian Distribution)

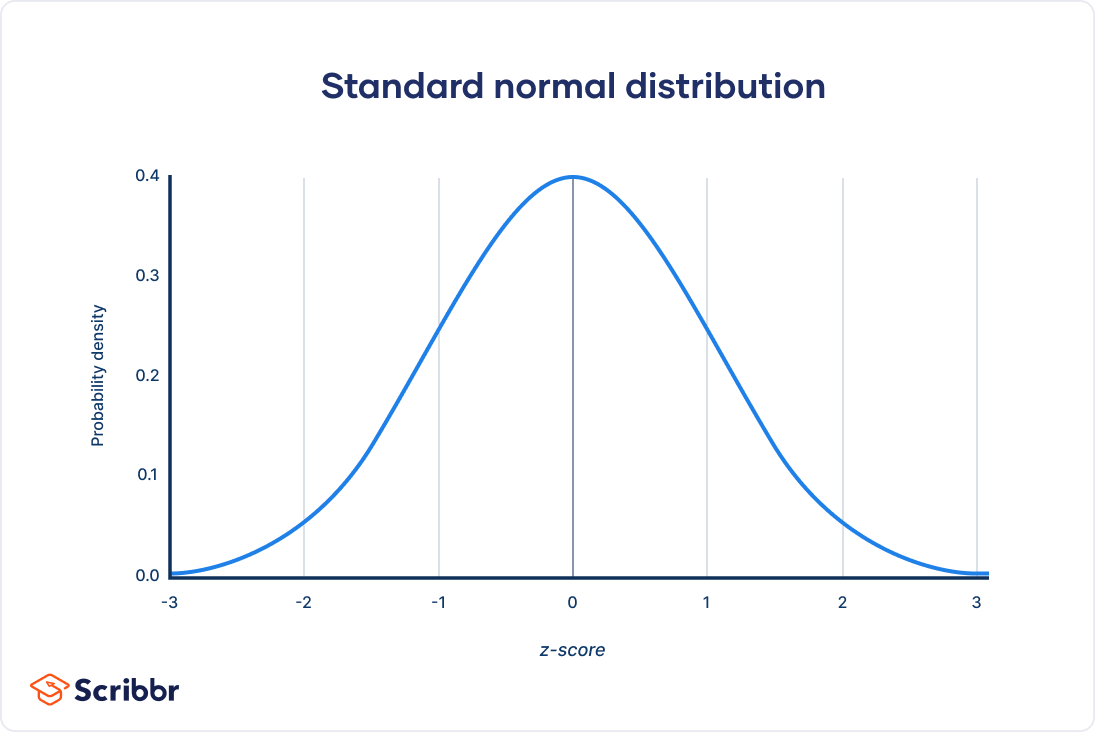
$image.png$

$p(x) = \dfrac{1}{\sqrt{2\pi \sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$

$X \sim N(\mu, \sigma^2)$