Transpose & Dot Product
1-4. 전치와 내적
전치(Transpose)
$ \begin{bmatrix}a_{11} & a_{12} \ a_{21} & a_{22}\end{bmatrix} ^T = \begin{bmatrix}a_{11} & a_{21} \ a_{12} & a_{22}\end{bmatrix} \implies \begin{bmatrix}A^T\end{bmatrix}{ij} = A{ji} $
전치의 성질
$\begin{bmatrix}a_{11} & a_{12} \ a_{21} & a_{22}\end{bmatrix}\begin{bmatrix}x_1\ x_2\end{bmatrix} = \begin{bmatrix}b_1\ b_2\end{bmatrix}$
$\implies \begin{bmatrix}a_{11}x_1+a_{12}x_2 \ a_{21}x_1+a_{22}x_2\end{bmatrix} = \begin{bmatrix}b_1 \ b_2\end{bmatrix}$
$\implies \begin{bmatrix}a_{11}x_1+a_{12}x_2 \ a_{21}x_1+a_{22}x_2\end{bmatrix} ^T= \begin{bmatrix}b_1 \ b_2\end{bmatrix}^T$
$\implies \begin{bmatrix}x_1 & x_2\end{bmatrix}\begin{bmatrix}a_{11} & a_{21} \ a_{12} & a_{22}\end{bmatrix} = \begin{bmatrix}b_1 & b_2\end{bmatrix}$
$\implies \overrightarrow{x}^TA^T = \overrightarrow{b}^T$
$\therefore (A\overrightarrow{x})^T = \overrightarrow{b} \iff \overrightarrow{x}^TA^T = \overrightarrow{b}^T$
내적(Dot Product)
$\begin{bmatrix}a_1 \ a_2\end{bmatrix}\bullet\begin{bmatrix}b_1 \ b_2\end{bmatrix} = a_1b_1 + a_2b_2 = \overrightarrow{a}^T\overrightarrow{b}$
→ 입력을 벡터로 받지만 내적의 출력은 스칼라값.
내적은 닮은 정도를 나타내기도 한다.
$\overrightarrow{a}^T\overrightarrow{b} = \mid\mid\overrightarrow{a}\mid\mid\,\mid\mid\overrightarrow{b}\mid\mid\,\cos\theta \enspace \text{where \mid\mid \mid\mid means L2 norm}$
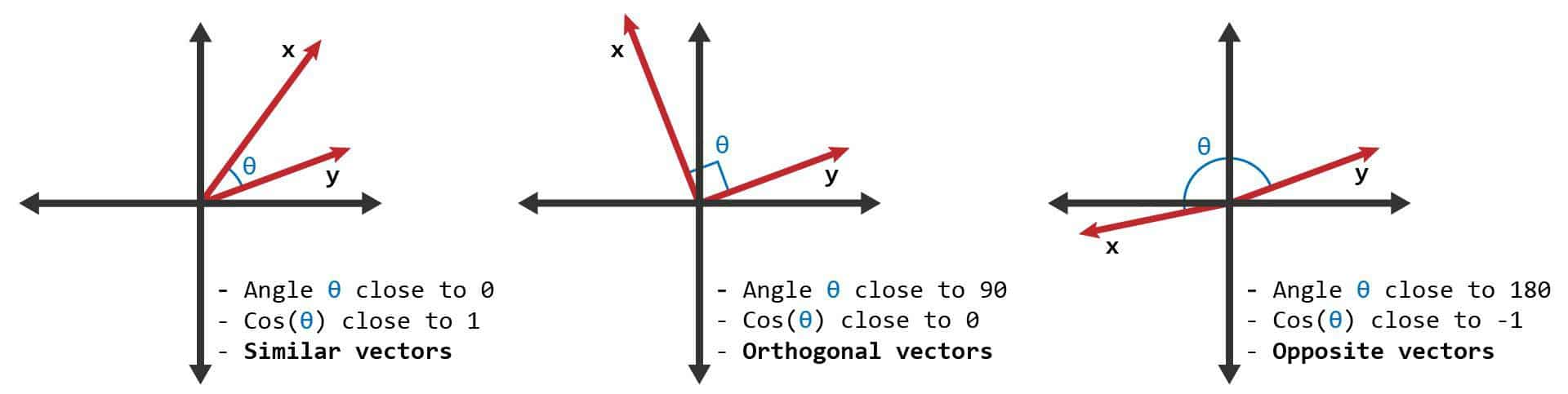
- 두 벡터가 겹칠 때 $\theta = 0$이므로 $\cos 0 = 1$이라는최댓값을 가지게 된다. 즉, 벡터가 닮을 수록 내적의 값이 커진다.
- 반대로 두 벡터가 직각일 때 $\cos 90 = 0$이므로 내적이 0이 된다.
- $\theta = 180$일때는 내적이 최솟값이지만 닮지 않은 건 아니고 음의 닮음이라고 정의한다.