Random Variable and Probability Distribution
1-17. 랜덤 변수와 확률 분포
랜덤 변수 (Random Variable, RV)
- 입력이 사건, 출력이 실수의 값
- 예) 동전 던지기 = 입력 / 앞면 : 1, 뒷면 : 0 = 출력
- 실수의 값을 확률 값으로 바꿔주는게 확률 함수
- 확률 질량 함수 (discrete / PMF) & 확률 밀도 함수 (continuous / PDF)
- 사건 → X(RV) → 실수 → P(PMF/PDF) → 확률
예시
- Coin Flip (PMF)
- $p_X(X = 0) = \frac12, \enspace p_{X}(X = 1) = \frac12$

- Dice Roll (PMF)
- $p_X(X = 5) = \frac 16 \cdots \enspace for \enspace x = 1 \cdots 6$
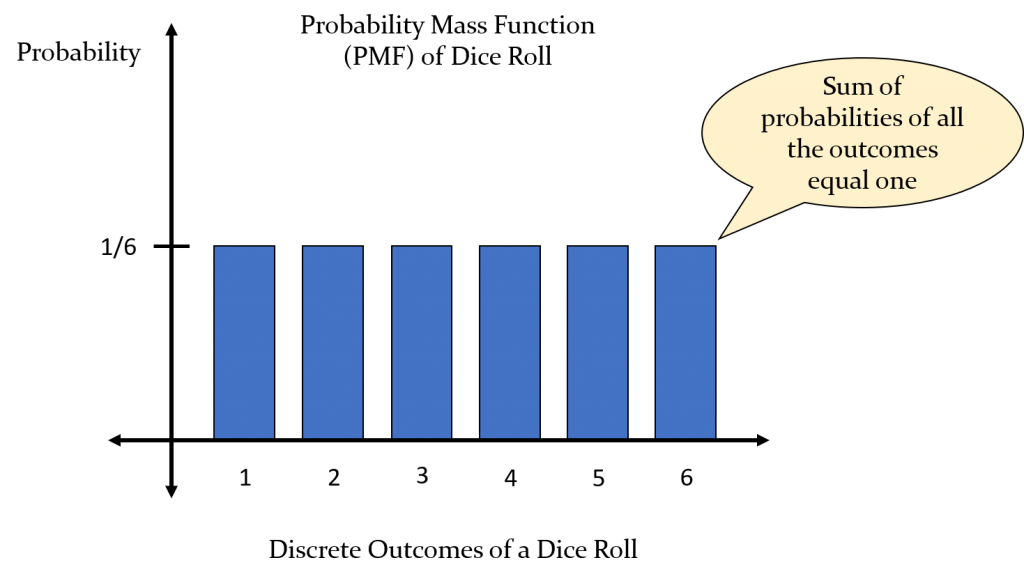
PMF 특징
- 값이 무조건 양수고 0과 1사이의 값이다.
- 합이 1이다.
PDF 특징
- 양수지만 0과 1의 사이일 필요는 없다.
- 적분이 1이다.
- 그래서 예를 들어 키가 165일 확률은 0이다. (적분은 범위가 필요하기 때문)