Maximum Likelihood Estimation
Maximum Likelihood Estimation (MLE)
Likelihood(우도)
A 주머니에는 까만 공 하나 흰색 공 하나가 들어있다.
B 주머니에는 까만 공 두개 흰색 공 하나가 들어있다.
$P(칠\mid A) = \frac12 \enspace P(칠\mid B) = \frac{2}{3}$
$P(안칠\mid A) = \frac12 \enspace P(안칠\mid B) = \frac{1}{3}$
- 가로로 읽는 것이 Likelihood라고 한다.
- $P(A\mid B)$일 때 B를 변수에 두고 보는 것.
- 그렇기 때문에 우도는 조건부 확률 값은 맞지만 확률 분포라고 말할 순 없다.
- 즉, 칠한 공을 꺼내고 싶을 때 어느 주머니에서 꺼낼까?
- 확률적으로 B 주머니에서 꺼낼 확률이 높다.
MLE (최대 우도 측정)
$Let \enspace z_1 = x+n ,\enspace z_2 = x+n_2 ,\enspace n \sim N(0, \sigma^2)$ → $n$은 Gaussian noise를 뜻한다.
→ $z_1$과 $z_2$를 보고 $x$를 예측하는 것이 MLE의 목표이다.
$P(z_1, z_2\mid x) = P(z_1\midx)P(z_2\midx)$ → 독립 시행 가정
$\hat x = \argmax\limits_{x} P(z_1, z_2\midx) = P(z_1\midx)P(z_2\midx)$ → 해당 값을 최대화하게 해주는 값이 우리가 원하는 $x$일 것.
$\hat x = \argmax\limits_{x} P(z_1, z_2\midx)$
$= \argmax\limits_{x}\dfrac{1}{\sqrt{2\pi\sigma^2}}e^{-\dfrac{(z_1-x)^2}{2\sigma^2}} \cdot \dfrac{1}{\sqrt{2\pi\sigma^2}}e^{-\dfrac{(z_2-x)^2}{2\sigma^2}}$
- 위의 식은 정규 분포를 따르고 정규분포에서 최대 값이 되는 부분의 미분 값은 0이 나온다. 즉, 미분해서 0이 나오는 $x$값이 $\hat x$이다.
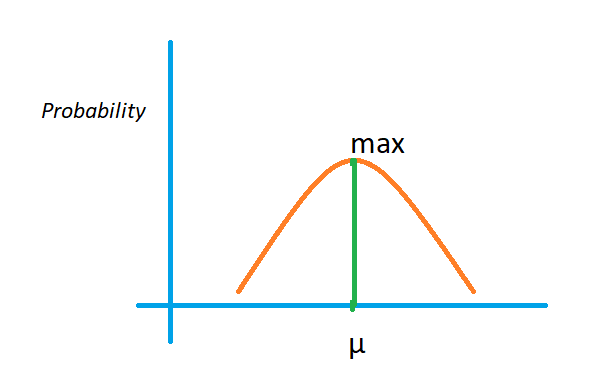
→ 쉬운 미분을 위해 로그 변환을 한다.
$\implies \log(\dfrac{1}{\sqrt{2\pi\sigma^2}}e^{-\dfrac{(z_1-x)^2}{2\sigma^2}} \cdot \dfrac{1}{\sqrt{2\pi\sigma^2}}e^{-\dfrac{(z_2-x)^2}{2\sigma^2}})$
→ $x$에 대해 미분을 하기 때문에 상수인 $\dfrac{1}{\sqrt{2\pi\sigma^2}}$을 제거한다.
$\implies \log e^{-\dfrac{(z_1-x)^2}{2\sigma^2}} \cdot \log e^{-\dfrac{(z_2-x)^2}{2\sigma^2}}$
$\implies -\dfrac{(z_1-x)^2}{2\sigma^2}-\dfrac{(z_2-x)^2}{2\sigma^2}$
→ 미분 진행
$\implies \dfrac{(z_1-x)}{\sigma^2} + \dfrac{(z_2-x)}{\sigma^2}$
→방정식으로 전환
$\implies \dfrac{(z_1-\hat x)}{\sigma^2} + \dfrac{(z_2-\hat x)}{\sigma^2} = 0$
$\implies z_1 + z_2 = 2\hat x$
$\therefore \hat x = \dfrac{z_1 + z_2}{2} = \argmax\limits_x P(z_1, z_2\midx)$
- 즉, measurement z에 gaussian noise가 첨가됐다면 각 $z_n$의 평균이 MLE의 관점에서의 $x$이다.
- 계산 과정에서 log가 아니라 -log를 취했다면 scale만 다른 MSE와의 식과 동일하다.