1-22. 정보 이론

Source Coding

  • 정보를 코드화해서 전달하는 기술
  • 하지만 정보는 랜덤하기에 이 코드를 최소화 시키기 어려움.
  • 자주 나오는 정보를 짧게 그리고 드물게 나오는 정보를 길게 코딩한다면 평균 코드 길이를 최소화 할 수 있음.

Entropy(엔트로피)

  • 이론적으로 entropy가 최소 평균 코드 길이이다.
  • 평균 길이 $= \sum_i p_il_i$
    • $p_i =$ i가 나올 확률
    • $l_i =$ i의 길이
  • 엔트로피 $= \sum_i-p_ilog_2p_i$

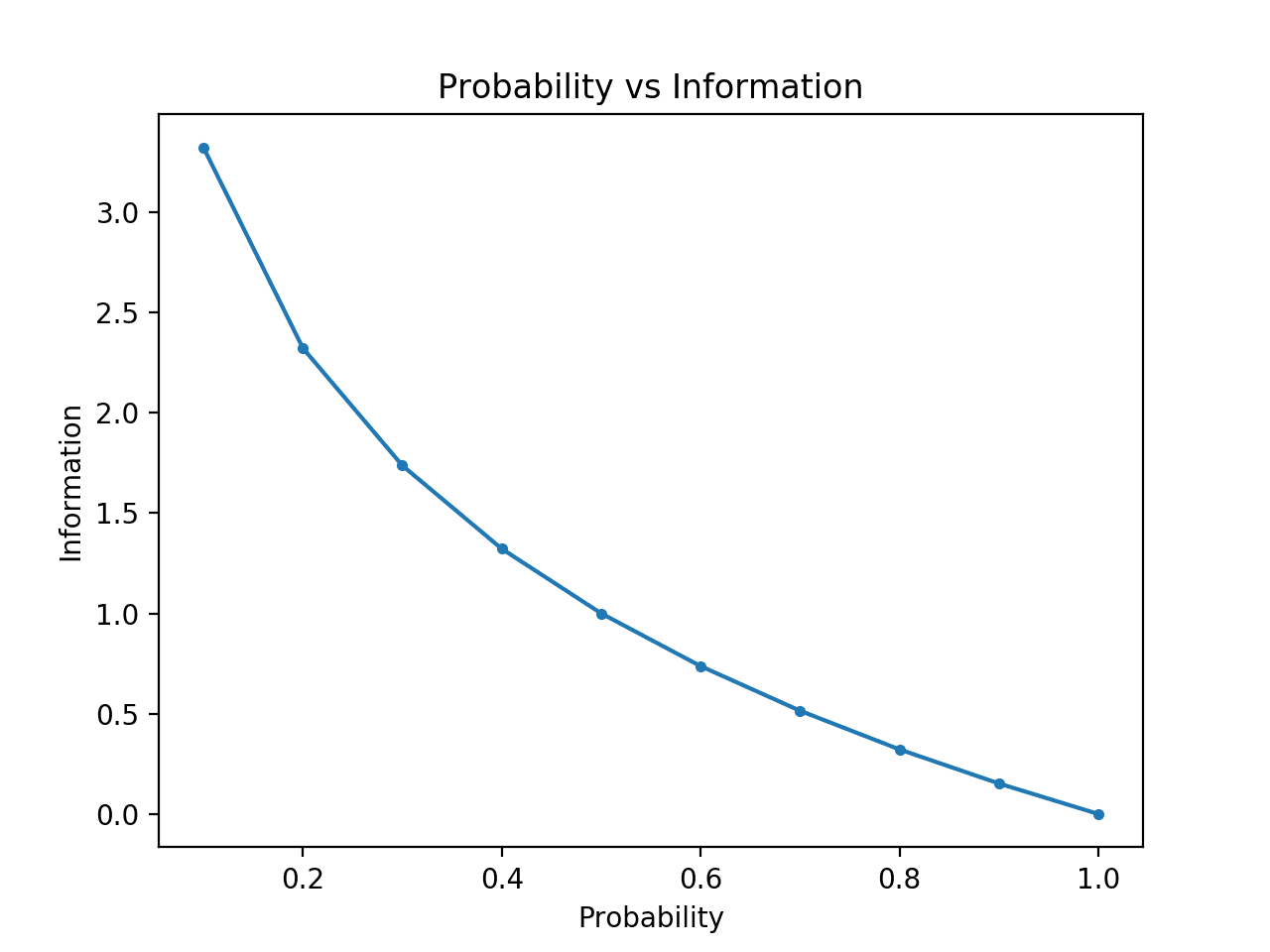
image 7.png

  • $l_i = -log_2p_i$ 라는 함수의 그래프이다.
  • $p_i$는 확률 값이기에 1보다 낮은 값만 보면 된다.
  • $p_i$가 높을수록 $l_i$ 즉, $log_2p_i$가 작아지고 $p_i$가 낮을수록 $l_i$가 커진다.
  • 그렇기에 $\sum_i-p_ilog_2p_i \leq \sum_i p_il_i$ 라는 lower bound가 생성된다.
  • 즉, source coding에서 균등분포는 최악의 상황이다.
  • 균등 분포의 entropy가 최대이고 $\sum_i p_il_i$는 어떠한 경우에도 entropy보다 낮을 수 없기 때문이다.

Cross Entropy (교차 엔트로피)

  • 엔트로피에서 $p_i$를 모른다면? 아니면 $-log_2p_i$가 정수가 아니라면?
    • 참고로 정보는 비트로 표현되기에 길이는 무조건 정수로 나온다.
  • 그래서 $p_i$대신 $q_i$를 사용한다.
  • $\sum_i-p_ilog_2q_i$
    • 무조건 엔트로피보다 값이 크다.
  • 딥러닝에서는 $q_i$가 신경망의 출력값이고 최대한 $p_i$와 비슷하게 만들려고 노력함.

KL Divergence

  • Cross Entropy와 Entropy의 차 (무조건 양수)
    • 교차 엔트로피의 값이 엔트로피보다 무조건 크기 때문이다.
  • $\sum_i-p_ilog_2p_i-\sum_i-p_ilog_2p_i \ = \sum_i(-p_ilog_2p_i + p_ilog_2p_i) \ =\sum_i-p_ilog_2\frac{p_i}{q_i}$
  • 엔트로피는 고정 값이기에 CE를 최소화하는게 KL을 최소화하는 것

Mutual Information

  • 두 분포의 독립적이지 않은 정도
  • $\sum -P(x_i, y_i)log_2\dfrac{P(x_i, y_i)}{P(x_i)P(y_i)}$
    • 두 분포가 독립이라면 $P(x_i, y_i) = P(x_i)P(y_i)$이기 때문에 값이 0이 나온다.

Updated: