Vanishing Gradient

7-1. Vanishing Gradient

층이 많아질수록 (깊어질수록) 입력 층에 가까울수록 미분 값이 사라진다. (0에 수렴한다)
Vanishing Gradient 말 그대로 그라디언트가 사라진다는 뜻이다.
- $W_{k+1} = W_k-\alpha\vec g$ 의 형태로 가중치가 업데이트 되는데 $\vec g$가 0으로 사라진다면 가중치는 더이상 업데이트 되지 않을 것이다.
그렇다면 왜 그라디언트가 깊어질수록 사라지나?
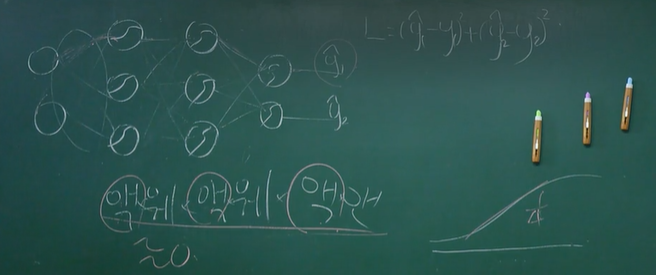
- 예를 들어 활성화 함수를 시그모이드를 사용한다고 가정하자.
- 위의 예시 같은 경우 마지막 가중치에 대한 편미분은 액,웨,액,웨,액,앤. 총 6개의 편미분이 곱해지는 형태가 된다.
- 하지만 시그모이드 함수의 최대 기울기는 $1\over4$ 이므로 이게 3번 곱해지면 거의 0에 수렴한 값일 것이다. 즉, 그라디언트가 사라지는 것이다.
결국 초반 가중치부터 vanishing gradient로 인해서 학습이 잘 안되니까 후반에 있는 가중치들도 난리가 나는 것이다.
결국 Underfitting이 되고만다.