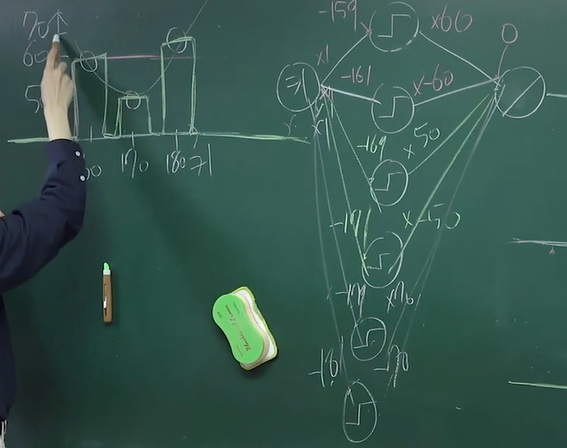6-1. Universal Approximation Theorem
인공 신경망의 구조에 대한 의문
- 인공 신경망의 구조는 입력 값이 들어오고 가중치가 곱해지고 편향이 더해진 후 활성화 함수를 통과하는 과정의 반복이다.
- 즉, 식으로 나타내자면 $f(f(\vec xW_1+\vec b_1)W_2+\vec b_2) \cdots$ 라는 형태로 나타나는데
- 과연 이런 형태가 고집되는 이유는 뭘까?
- Universal Approximation Theorem을 통해 증명할 수 있다.
Universal Approximation Theorem
- 해당 이론은 은닉 층이 딱 하나만 있으면 어떠한 연속 함수더라도 나타낼 수 있다는 이론이다.
- 예시를 통해 위의 이론을 한번 증명해보자.
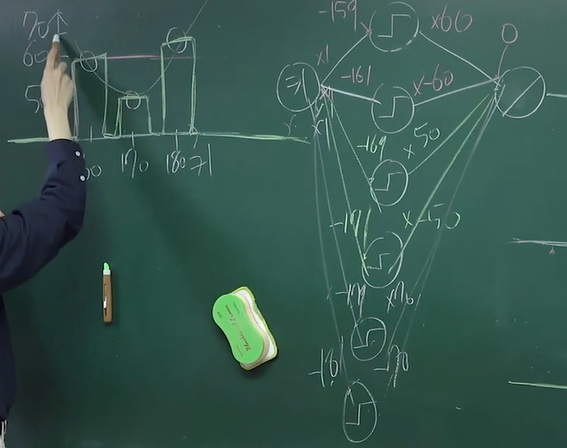
- 키가 160일때 몸무게는 60, 170일때는 50, 180일때는 70이라는 세 개의 데이터를 표현 할수 있는 모델을 만들어보자.
- 은닉 층은 1개만 존재하며 활성화 함수는 Unit Step을 사용한다.
- 가중치는 모두 1이라고 통일하고 첫번째 노드에 대한 편향치가 -159라고 하자. 이후 출력 층에 대한 가중치는 60이라고 하고 편향치는 0이라고 하자.
- 그러면 160이 입력 일때 $(160-159) * 60 + 0 = 60$ 이라는 값이 도출 된다.
- 즉, 키가 160 이상이면 60이라는 값이 출력되는 것이다.
- 이후 두번째 노드에 대한 편향치는 -161, 출력 층에 대한 가중치는 -60, 편향치는 0이라고 한다면 $(160-161)*-60+0 = -60$이라는 값이 도출 된다.
- 최종 출력에서는 은닉 층에 있는 모든 노드의 출력 값이 더해지기 때문에 160에서만 출력이 60이고 나머지 수에서는 0이 출력되는 함수를 만들어낸다.
- 이런 식으로, 170일때는 50, 180일때는 70만 나오게끔 노드를 추가하며 만들면 은닉 층 하나만으로도 원하는 함수를 만들어낼 수 있게된다.
- UAT는 Unit Step에서만 되는 것이 아니라 시그모이드도 얼마든지 활용하여 모든 함수를 나타낼 수 있다.
- 그리고 입력이 여러 개이고 출력이 여러 개 일때도 사용 가능하다.
Universal Approximation Theorem의 문제점
- Softmax같은 출력을 은닉 층 하나로는 나타내기 상당히 복잡하다.
- 노드만 너무 많아지면 너무 비효율적이다.
- FC Layer는 사실 비효율 모델이다.