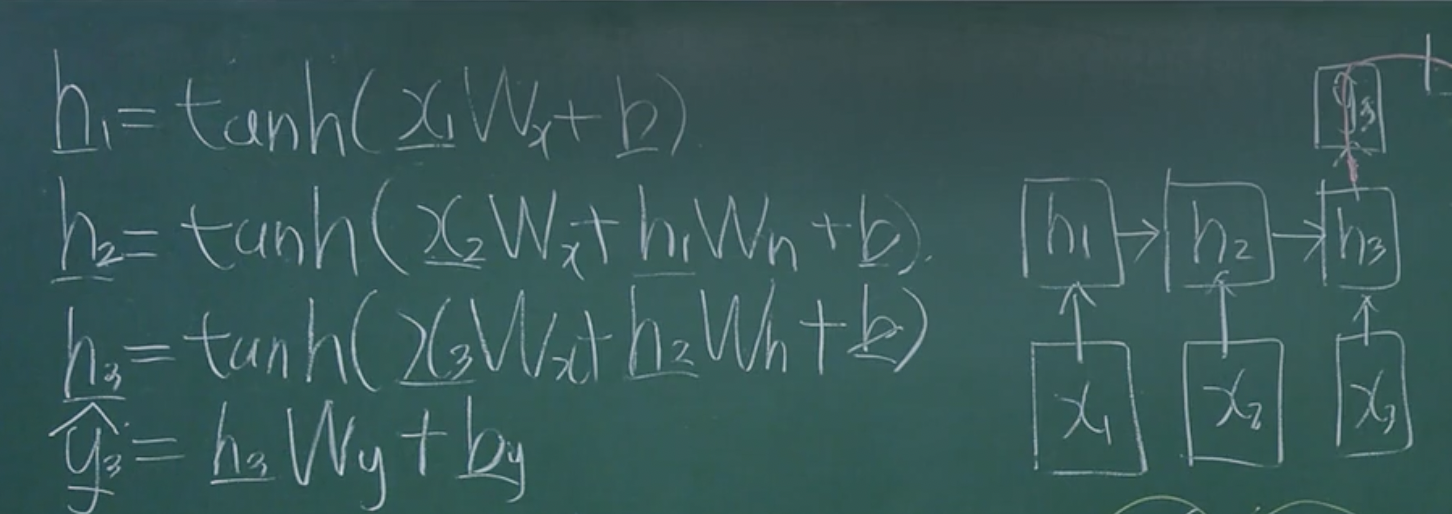9-2. RNN Back Propagation
RNN의 손실 함수
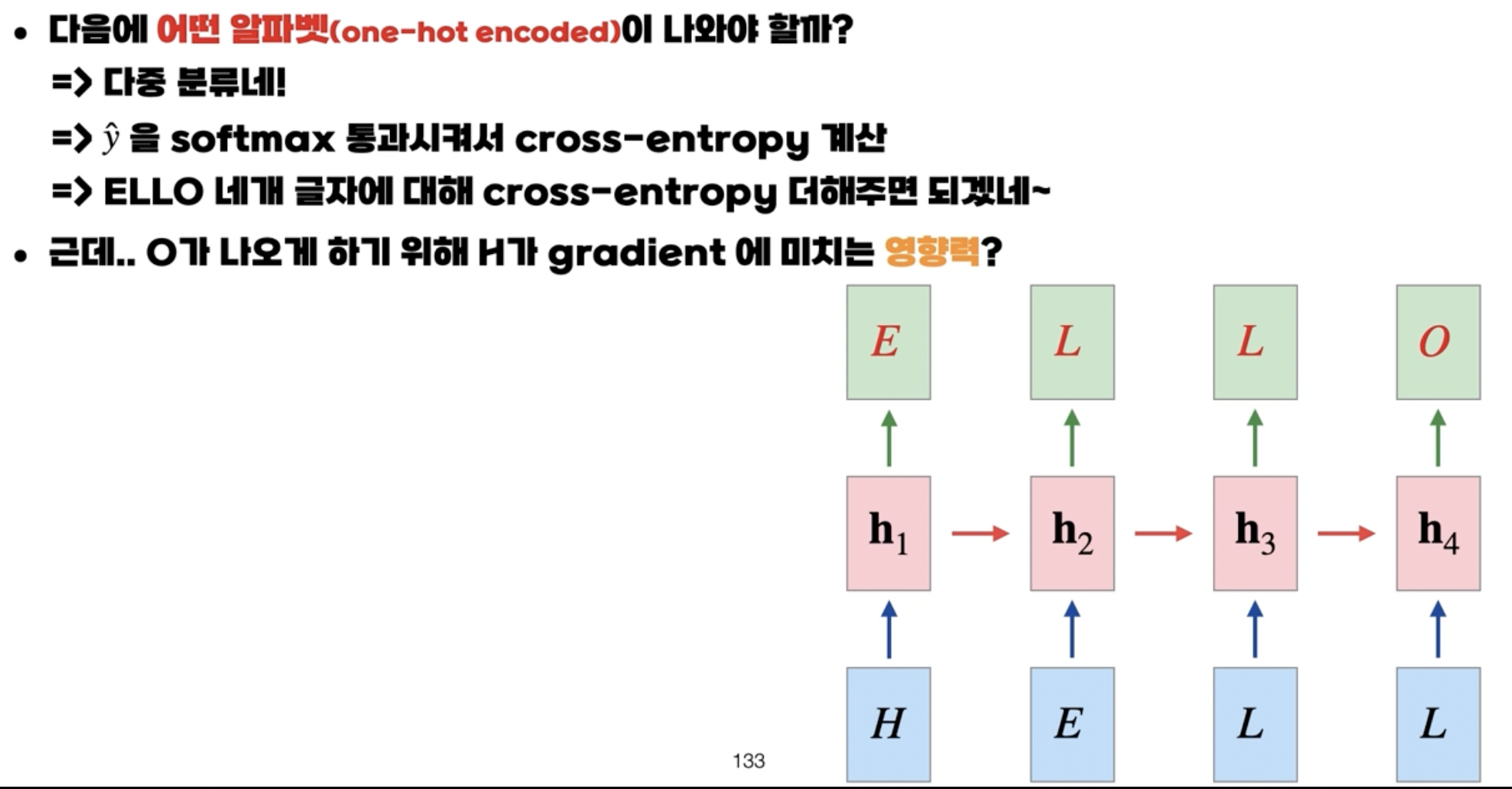
- HELL이라는 입력에서 마지막에 O라는 글자가 나오도록 하는게 해당 모델의 목표다.
- 즉, 알파벳을 맞추는 것이기 때문에 다중 분류 문제에 속하게 되고 손실 값은 교차 엔트로피가 된다.
- 그렇다면 역전파를 통해 H가 그라디언트에 미치는 영향력을 살펴보자
RNN의 역전파
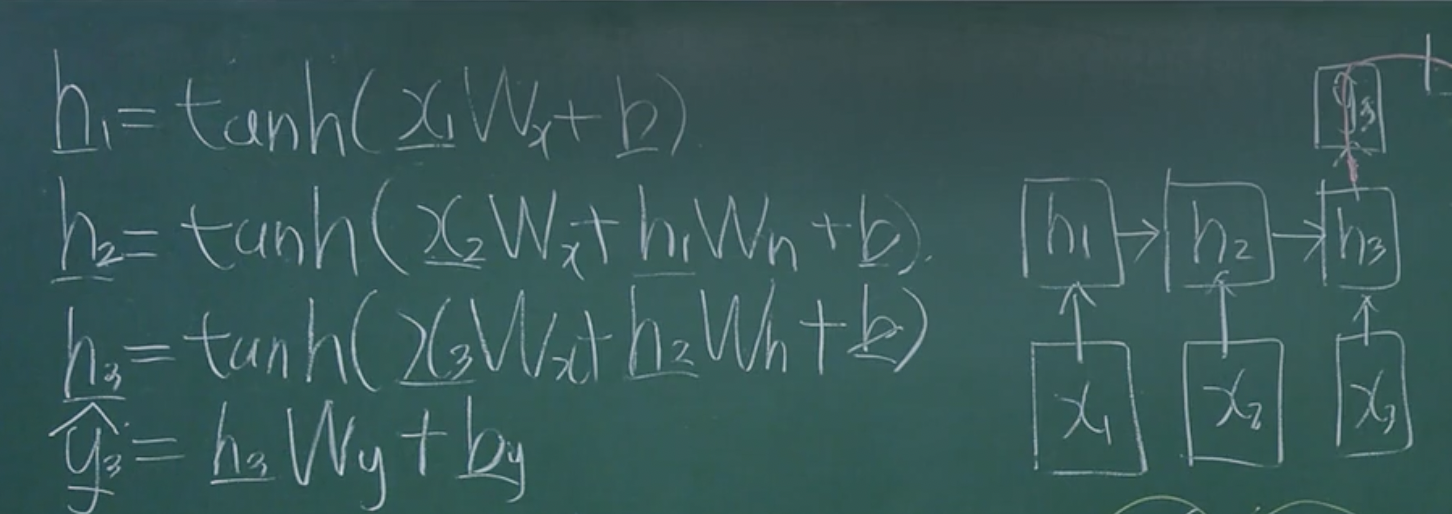
- 예시로 3번째 단계까지만 있는 RNN이라고 하자.
- 학습되는 파라미터는 $W_x, W_h, W_y, \vec b, \vec b_y$ 총 5개이지만 가중치만 편미분을 해보자.
- $W_y$의 편미분
- $\dfrac{\partial L}{\partial W_y} = \dfrac{\partial L}{\partial \hat y_3}\dfrac{\partial \hat y_3}{\partial W_y}$
- $W_h$의 편미분
- $\dfrac{\partial L}{\partial W_h} = \dfrac{\partial L}{\partial \hat y_3}\dfrac{\partial \hat y_3}{\partial h_3}\dfrac{\partial h_3}{\partial W_h} + \dfrac{\partial L}{\partial \hat y_3}\dfrac{\partial \hat y_3}{\partial h_3}\dfrac{\partial h_3}{\partial h_2}\dfrac{\partial h_2}{\partial W_h}$
- $W_h$가 쓰이는 곳이 두 곳이므로 두 곳 다 편미분 진행 후 덧셈
- $W_x$의 편미분
- $\dfrac{\partial L}{\partial W_x} = \dfrac{\partial L}{\partial \hat y_3}\dfrac{\partial \hat y_3}{\partial h_3}\dfrac{\partial h_3}{\partial W_x} + \dfrac{\partial L}{\partial \hat y_3}\dfrac{\partial \hat y_3}{\partial h_3}\dfrac{\partial h_3}{\partial h_2}\dfrac{\partial h_2}{\partial W_x} + \dfrac{\partial L}{\partial \hat y_3}\dfrac{\partial \hat y_3}{\partial h_3}\dfrac{\partial h_3}{\partial h_2}\dfrac{\partial h_2}{\partial h_1}\dfrac{\partial h_1}{\partial W_x}$
- 결국 액 * $x_3$ + 액 * 웨 * 액 * $x_2$ + 액 * 웨 * 액 * 웨 * 액 * $x_1$의 형태가 나온다.
- 하지만 $x_1$에 대해서는 곱해지는 값들이 너무 많아 그라디언트에 대한 영향력이 얕아진다.
RNN의 구조적 한계점
파이썬 실습
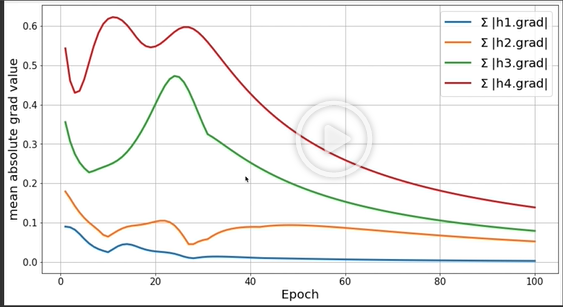
- 파이썬 코드로 실제로 RNN을 돌려본 결과이다.
- $h_4$부터 $h_1$까지 갈수록 그라디언트 값이 줄어들고 $h_1$은 거의 0에 수렴하는 것을 볼수가 있다.