7-2. ReLU (Rectified Linear Unit)
ReLU 함수의 개념
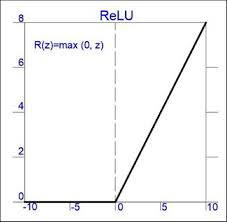
- ReLU는 음수에 대한 입력은 모두 0을 출력을 하고 0 이상의 입력 값은 그대로 내보내준다.
Vanishing Gradient의 해결법
- Vanishing Gradient 문제에 대한 주범은 기울기가 최대 $1\over4$ 밖에 되지 않는 시그모이드 함수였다.
- 인공 신경망이 깊어질수록 편미분이 계속 곱해지면서 그라디언트가 0으로 수렴할수 밖에 없어진다.
- 하지만 ReLU는 0이상의 값에 대해선 기울기가 1이기에 그라디언트가 사라지진 않는다.
- 하지만 음수에 대한 입력 값은 0을 출력하기에 그라디언트가 0으로 사라지지 않냐? 라는 의문이 들수 있다.
- 그렇지만 모든 입력 값이 음수이지 않는 이상 그라디언트가 0으로 변할 일은 없다.
- 각각의 루트에 대한 편미분을 더해줘야하기에 그럴 확률은 희박하다.
Leaky ReLU / Parametric ReLU
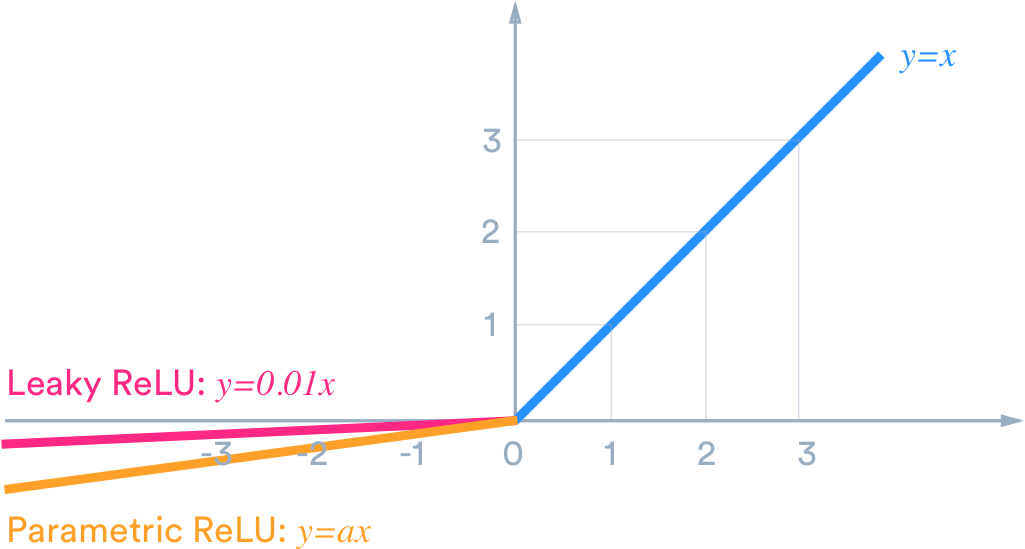
- 음수 입력값에 대한 기울기를 살리기 위해서 0.01만큼의 기울기를 준 것이 Leaky ReLU이다.
- Parametric ReLU는 음수 입력값에 대한 기울기도 학습을 통해 정한다는 개념을 도입한 것이다.
- 그렇다면 그냥 음수 입력에 대한 기울기도 1로 두면 안되나?
- 그러면 결국은 Linear Activation 함수가 되어버리고 이는 인공신경망의 장점인 non-linearity를 잃어버리게 하는 행위임으로 전혀 의미가 없는 행동이 되어버린다.

