Perceptron

5-1. 선형분류와 퍼셉트론

Non-Linear Activation을 이용한 이진 분류

• 예시 문제
  • 입력 : 키와 몸무게
  • 출력 : 1(빼야 할 사람), 0 (쪄야될 사람)

• 사용할 비선형 활성화 함수는 Unit Step Function이다.

  

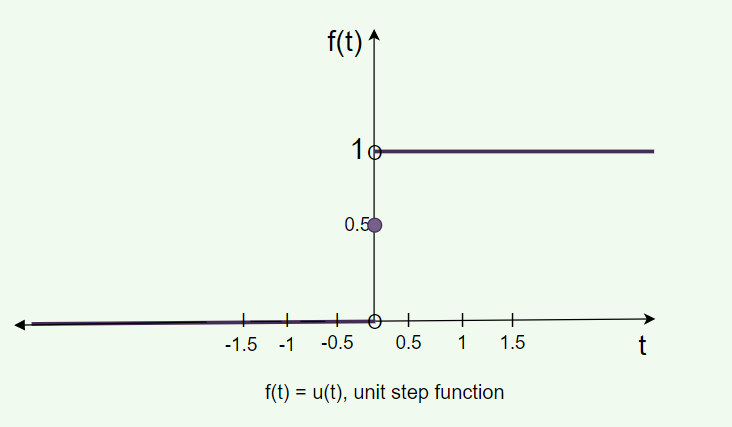
• 해당 활성화 함수를 사용하고 입력 층이 활성화를 통과하여 바로 출력이 나온다면 선형 분류에 사용이 가능하다.
  • 즉, 퍼셉트론은 선형 분류가 가능하다.
  • 선형 분류란 분류하는 경계선이 선형이라는 뜻이다.
• 하지만 Unit Step은 미분이 가능한 함수가 아니기에 경사 하강법으로 파라미터를 찾는 것을 불가하다.
• 그렇기 때문에 가중치와 편향을 이용하여 간단하게 동작 원리만 알아보자.
  • 키에 대한 가중치는 -1, 몸무게에 대한 가중치는 1이라고 하고 편항은 -1이라고 하자.
  • 키를 $x$, 몸무게를 $y$라고 할때 $-x+y-1$이라는 값이 활성화 함수를 통과하게 된다.
  • Unit Step 함수 이기 때문에 $-x+y-1>0$이라면 1이라는 값을 출력할것이다.
  • 즉, $y = x+1$이라는 분류 경계선이 생긴다.
• 해당 예시는 2개의 입력, 2개의 출력을 가지기 때문에 2차원 상이 아니라 3차원 상으로 봐야된다.

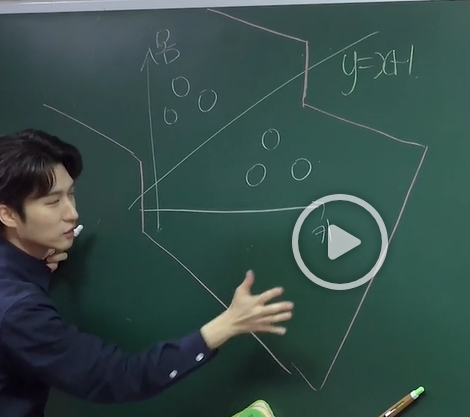
• 이와 같이 1이 출력되는 구간과 0이 출력 되는 구간이 명확하게 나뉘어져보인다.

• 즉, 선형 분류지만 비선형의 출력이 나온다.
• 이러한 모델의 단점은 미분이 불가하고 경계가 너무 tight 하다는 것이다.

시그모이드 활성화 함수

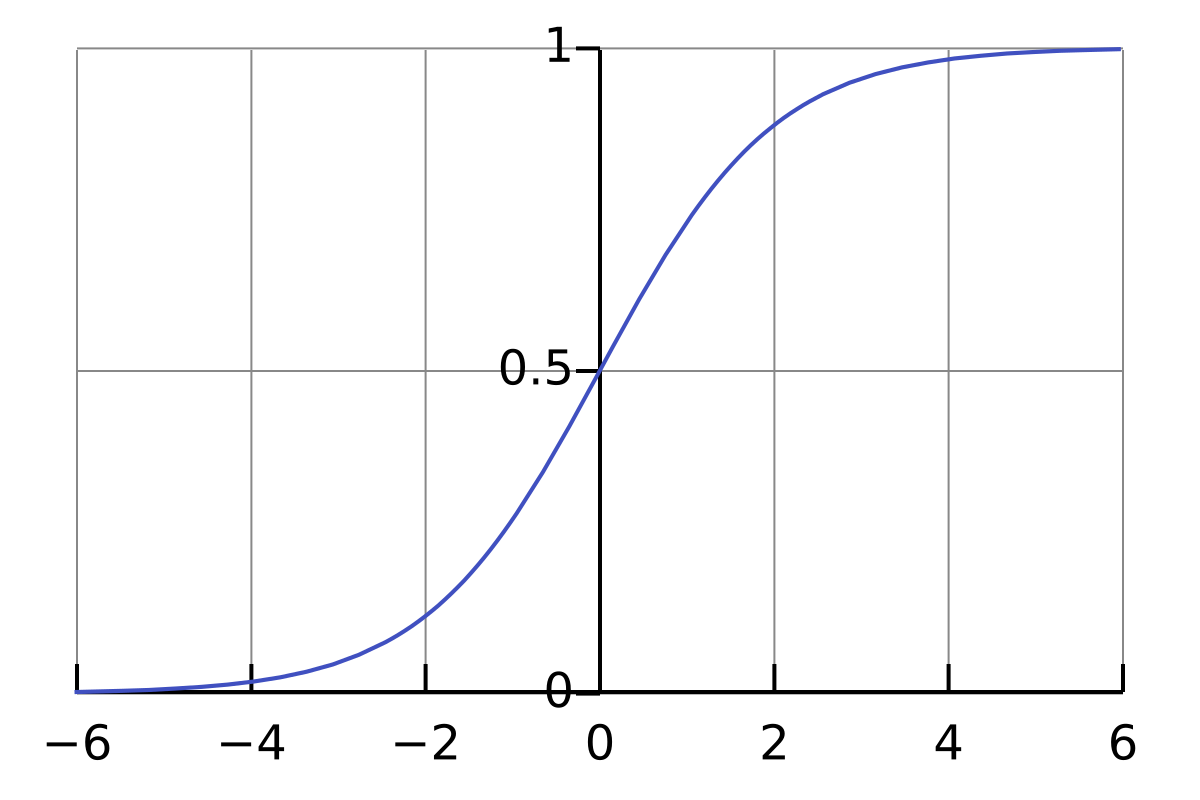
• Unit Step의 단점을 해결하기 위해 나온 활성화 함수이다.
• Unit Step의 부드러운 버전.
• 미분이 가능하고 조금 더 부드러운 분류가 가능하다.
• $\dfrac{1}{1+e^{-x}}$

• 최대 기울기 즉, 최대 미분 값은 $1\over4$이다.

• 만약 위의 예시를 Unit Step이 아니라 시그모이드를 사용하면 이와 같은 결과가 나온다.
• 출력 값이 0과 1 두개가 아니라 0과 1사이의 모든 실수가 출력 값의 범위가 된다.
• 즉, 출력의 해석을 확률 또는 정도라는 개념으로 볼수 있게 된다.

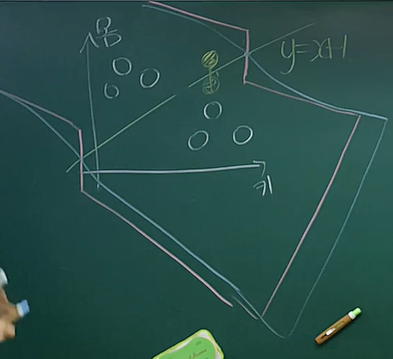
• 좌측의 그림을 보면 1번 선과 2번 선은 Unit Step으로 나올 수 있는 경계선인데 퍼셉트론 한테는 1번과 2번의 경우 둘 다 완벽한 분류를 했다고 판단한다.

• 하지만 시그모이드는 1번에 가까울 수록 0.55 같은 값을 내놓아서 해당 입력 값이 1에 가까워질수 있도록 파라미터를 업데이트 해줄 수 있다.