Neural Network
3-1. 인공 신경망
뉴런
- 생체적 뉴런은 어떠한 자극을 받고 그 자극을 다른 뉴런에게 전달할지 안 할지를 결정한 이후 결정이 난 행동을 취한다.
- 이러한 행동을 인공적으로 컴퓨터가 시행할 수 있도록 만든 것이 인공 신경망이다.
인공 뉴런
-
‘뒷통수’라는 입력 노드와 ‘손바닥’이라는 입력 노드가 있다. 이 들은 고통이 없으면 0, 고통이 있으면 0이상의 실수로 값을 입력 받는다.
-
이후 입력 노드는 활성화 함수 라는 것을 거치는데 이는 많은 종류가 있지만 여기 예시에서는 step function이라는 활성화 함수를 쓴다.
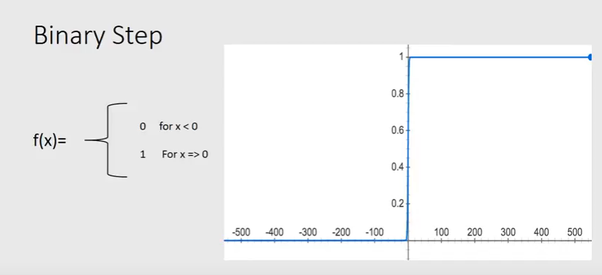
- 하지만 이럴 경우 아주 조그마한 자극이 있어도 출력 값이 1로 나온다.
- 여기서 출력 값 1의 의미는 위기라는 것을 알려주는 것이다.
- 그래서 도입 되는 것이 Bias이다. bias는 민감도 같은 것으로 조그마한 입력 노드의 변화로는 활성화 함수가 활성화 되지 않게 해주는 것이다.
- 예를 들어 bias가 -2이면 입력 노드의 값의 합이 1이면 출력값이 0으로 활성화되지 않는다.
- 하지만 입력 노드마다의 중요도를 구현해주기 위해 weight라는 개념이 추가된다.
- 즉, 입력 노드마다의 weight를 곱해주고 bias를 더해주는 것이 최종적으로 활성화 함수에 들어가는 입력 값이라는 것이다.
- 예를 들어 ‘뒷통수’노드에 1이라는 값이, 그리고 ‘손바닥’노드에 0이라는 값이 입력되어있는데 뒷통수의 weight값이 10이고 bias가 -2이면 101+10-2 = 8이라는 값으로 활성화 함수가 1이라는 출력 값을 내놓는다.
- 즉, 주어진 입력에 따라 원하는 출력 값이 나오도록 weight와 bias를 조절해줘야한다.
- 결국 AI가 해야되는 작업이 원하는 값이 나오도록 적절한 weight와 bias를 찾는 것이다.
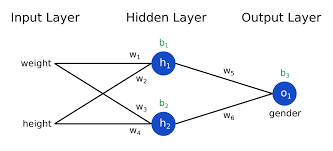
인공 신경망
- 인공 뉴런들의 집합체라고 보면 간단하다.
- 위에서 설명한 인공 뉴런의 입력 노드가 활성화 함수 노드로 바뀌고 그 전에 입력 노드를 받으면 그게 인공 신경망이다.
- 인공 신경망의 깊이는 무한정 가능하다.
- 입력층 (즉, 입력 노드들)은 1개 밖에 존재하지 않는다.
- 입력층에서 받은 입력 노드의 값들을 각각 weight를 곱해주고 bias를 더해주고 activation에 통과시켜준다. 그 이후 나온 출력 값을 또 weight를 곱해주고 bias를 더해주고 activation에 통과… 이 과정을 마지막 출력 층 까지 반복해준다.
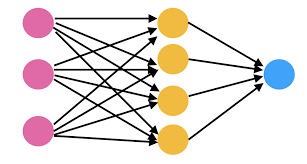
핑크 색이 입력 층, 노란 색이 은닉 층, 파란 색이 출력 층이다.
- 입력 층의 노드가 3개, 그 다음 은닉 층의 노드가 2개, 출력 층의 노드가 1개일 때의 weight와 bias 갯수를 세보자
- 입력 층에서 은닉 층으로 갈 때의 weight 갯수는 (입력 층의 노드 갯수) * (은닉 층의 노드 갯수). 즉, 3 * 2 = 6개이다.
- 입력 층에서 은닉 층으로 갈 때의 bias 갯수는 은닉 층의 노드 갯수와 동일하므로 2개이다.
- 같은 방식으로 은닉 층에서의 출력 층으로의 weight 갯수는 2*1 = 2개이며 bias 갯수는 1개이다.
추가 정보
- 은닉 층이 많은 인공 신경망을 DNN (Deep Neural Network)라고 한다.
- Unit Step Function을 활성화 함수로 사용하는 단일 신경망을 Perceptron이라고 한다.
- 층 마다 모든 노드가 연결되어 있는 신경망을 Fully Connected (FC) Network라고한다.
- 모든 층이 FC layer인 신경망을 MLP (Multilayer Perceptron)이라고 한다.
인공 신경망은 함수다
- 다시 말해, 인공 신경망은 입력과 출력을 연결시켜 주는 연결 고리 인것이고 결국 주어진 입력에 대해 원하는 출력이 나오도록 하는 함수를 알아내자는 것.
- 바로 그 함수를 인공 신경망으로 표현했으니 weight, bias를 알아내는 것이 딥러닝의 목표이다.
- 조금 더 자세히 이해하기 위해 $ax+b$라는 1차 함수를 인공 신경망으로 표현하자.
- 입력 층에는 $x$가 들어가고 weight대신 $a$라는 변수 그리고 bias를 b라고 표현을 하자.
- 그러면 활성화 함수에 들어가기 전 변화 된 입력 값은 $ax+b$이다.
- 입력 값과 똑같은 값을 출력해주는 활성화 함수는 linear activation이라고 부른다.
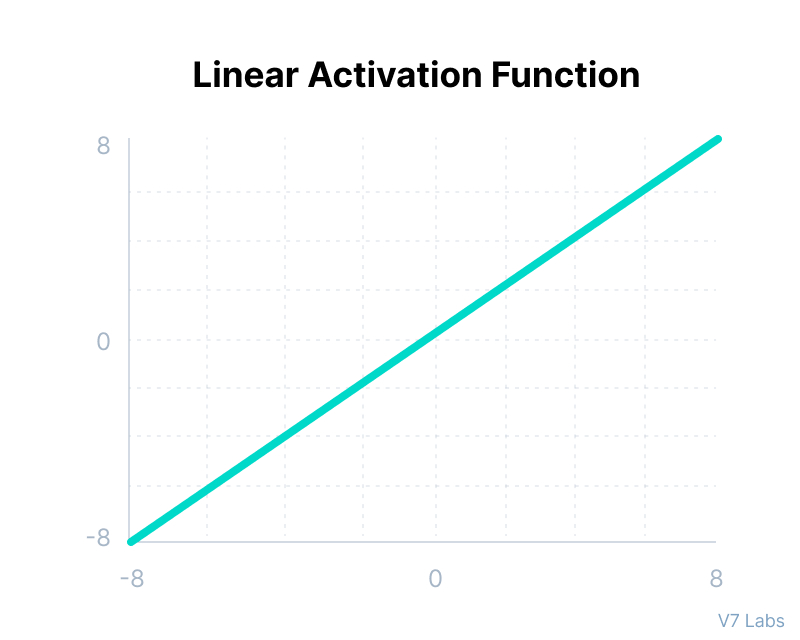
- 해당 활성화 함수를 통과 시키면 $ax+b$를 인공 신경망으로 표현할 수 있다.