MSE vs. Likelihood

5-3. MSE vs. Likelihood

MSE vs. Likelihood

• 5-2강에서의 예시 문제를 생각해보자.
• 3x100x100 사이즈의 사진을 강아지 또는 고양이로 분류하는 문제이다.
• 활성화 함수는 시그모이드를 활용을 한다.

손실 함수 형태의 문제점

• MSE를 활용하면 $q=1$의 상황에서 $(q-1)^2$을 minimize하는 것이 목표이고
• Log-likehood를 사용하면 $-\log q$를 minimize하는 것이다.

• 흰색 선이 MSE의 상황이고 분홍색 선이 Log-likelihood의 상황이다.
• 보다 싶이 모델이 0이라고 예측하면 MSE는 손실 값이 1이라고 출력하는 반면, Likelihood는 무한대로 발산해버린다.
• 즉, Log-likelihood가 오류에 더욱 민감하다는 것이다.

손실 함수 최적화의 문제점

• 결론부터 말하자면…
  • MSE는 non-convex의 형태를 띄고
  • Log-likelihood는 convex의 형태를 띈다
• Non-convex의 경우 local minimum이 global minimum과 다르기에 로컬에서 머무를 수 있다는 단점이 있다.

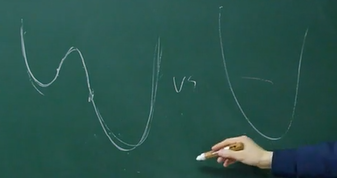
왼쪽이 non-convex, 오른쪽이 convex

• 입력 값이 1이고, 가중치가 W고, 편향이 0이라고 가정을 하자.
• MSE의 경우,
  • $q = (\dfrac{1}{1+e^{-W}}-1)^2$ 이라는 손실 함수를 만들어내고
• Log-likelihood의 경우,
  • $q = -\log\dfrac{1}{1+e^{-W}}$ 이라는 손실 함수를 만들어낸다.

• 그래프를 그려보면…

  

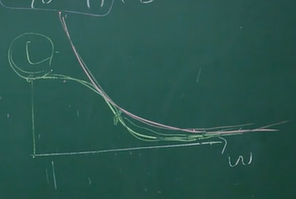
  • 흰색 선이 MSE, 분홍색 선이 log-likelihood를 나타낸다.
• 물론, 층이 깊어 질수록 두 경우 다 non-convex해지긴 하지만 MSE의 경우 non-convex의 정도가 심해진다. 즉, 로컬에 빠질 확률이 높아진다는 것이다.