5-2. Binary Classification w/ Sigmoid
예시 문제
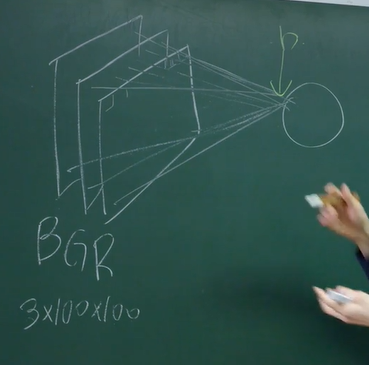
- 3x100x100이라는 사진이 입력 값이고 출력이 곧 바로 나온다고 가정하자.
- 각각의 픽셀에 가중치가 곱해지고 마지막에 편향이 더해져서 시그모이드 활성화 함수를 통과한다.
- 출력 값인 $q$가 사진이 강아지일 확률을 나타내고 강아지면 $q = 1$, 고양이면 $q = 0$.
- 정답 출력 값은 $y$라고 하자.
- 손실 함수를 정의해보자면…
- 사진이 강아지일 때는 ($q = 1$), $q$를 maximize하면 되고
- 사진이 고양이일 때는 ($q = 0$), $1-q$를 maximize하면 된다.
- 즉, $q^y(1-q)^{1-y}$를 손실 함수로 두고 이를 maximize하면 된다.
- 인덱스를 지정해주어 i번째 사진은 $q^{y_i}_i(1-q_i)^{1-y_i}$ ⇒ 머신이 예측한 정답 레이블일 확률
- 하지만 위의 함수는 문제가 있다.
- 각각의 사진 데이터는 독립 시행이므로 정답 레이블일 확률이 곱해지는데 시그모이드 함수를 통과했으므로 0과 1사이의 값이 계속 곱해진다.
- 이는 곱해질수록 0으로 수렴하므로 문제가 된다.
- 하지만 로그를 취해주면 로그의 성질로 인해 각각의 곱은 덧셈으로 바뀌므로 위의 문제를 해결할 수 있다.
- 즉, $L = -\sum_i\log(q_i^{y_i}(1-q_i)^{1-y_i})$라는 손실 함수를 가중치에 대해서 미분해서 반대 방향으로 나아가면 된다.
- 하지만 로그를 취해도 아무 이상이 없나?
- 이상 없다. 이유는 log(L)이 줄어도 L이 같이 줄어들기 때문.
- 이를 Monotonic Increase (단조 증가)라고 한다.
Logistic Regression
- 위에 설명한 예시들은 사실 Logistic Regression이라고 불리는 모델이다.
- 사실 분류도 regression이다.
- Logistic Regression이란 무엇이냐?
- Logit을 Regression한 것이다.
- Logit은 log-odds. 직역하자면 log 승산이라는 뜻이다.
- $\text{logit} = \log \dfrac{q}{1-q} = l$
- 예를 들어 위에서 언급한 사진 데이터를 linear activation 시킨 걸 logit이라고 하자.
- 그 이후 logit을 시그모이드를 통과시키면 우리가 아는 q값이 나온다.
- 이에 대한 증명을 해보자면…
- $\log \dfrac{q}{1-q} = l$
- $\dfrac{q}{1-q} = e^l$
- $\dfrac{1}{q}-1 = e^{-l}$
- $\therefore q = \dfrac{1}{1+e^{-l}}$
