Batch Normalization

Batch Normalization (BN)

배치 사이즈가 5라고 가정하고 활성화 함수가 ReLU라고 가정하자.
배치 사이즈가 5이므로 데이터 5개가 ReLU를 통과할텐데 여기서 5개가 다 양수 혹은 음수면 어떡하나?
- 5개 다 양수인 경우는 결국 linear activation과 다를게 없다. 즉, non-linearity를 잃는다.
- 5개 다 음수인 경우도 결국 x축을 따라가기에 linear activation과 다를게 없고 기울기가 0이기에 vanishing gradient 문제도 생기게 된다.
그러면 아예 들어온 데이터를 재배치 시키자.
- 들어온 데이터가 음수와 양수 모두 포함시키게 재배치 시키면 된다.
한층 더 나아가서 그냥 평균이 0, 분산이 1이 되도록 normalization 시키면 어떨까?
- 좋은 아이디어이지만 sigmoid의 경우 가운데에 데이터가 몰려있을수록 non-linearity를 잃기때문에 오히려 성능 저하가 일어난다.
그러면 어디에 재배치 시키는게 좋은 걸까?
- 그러면 어디에 재배치시킬지 학습하도록 하자.

Normalization을 진행할 때 다음과 같은 식을 통과하게 된다.
- $\dfrac{X-\bar X}{\sigma_X}$
- 즉, 평균을 빼주고 표준 편차를 나누어줌으로써 평균이 0, 분산이 1로 바뀌는 것이다.
그렇다면 여기서 평균과 분산을 자유롭게 컨트롤하려면 어떻게 해야할까?
- a와 b라는 변수를 넣어주는 것이다.
- $a(\dfrac{X-\bar X}{\sigma_X})+b$
- 위의 식에서 평균을 구하자면…
  - $E[aY+b] = aE[Y]+b = b$
  - $E[Y]$는 normalize를 했기 때문에 0이다.
- 위의 식에서 분산을 구하자면…
  - $V[aY+b] = a^2V[Y] = a^2$
- 즉, 원하는 평균과 분산을 맞추기 위해서는 a와 b의 값을 조정해주면 된다.
결국 $a(\dfrac{X-\bar X}{\sigma_X})+b$은 미분이 가능하기 때문에 학습을 통해 non-linearity를 살려주고 vanishing gradient를 없애주는 a와 b의 값을 찾아주면 된다.

BN에서는 활성화 함수가 들어있는 노드마다 a,b를 학습시켜야하지만 Layer Normalization은 층 전체에 대한 a,b를 통일시켜 학습시키는 것이다.
BN에서는 만약 배치 사이즈가 1이라면 분산이 0이기 때문에 normalization 자체가 되지 않는다.
이러한 문제점을 해결하기 위해 LN이 도입 되었다.
LN은 배치의 개념은 전혀 없고 데이터 1개씩만 인공 신경망을 통과한다.
이때 만약 층의 노드가 3개라면 해당 층에 들어가는 입력 값은 3개이므로 이 3개의 데이터에 대한 평균과 분산의 위치를 계산할 a,b를 학습시키는 것이 LN이다.
즉, 해당 층에 대해 얼마나 non-linearity를 살릴지, 얼마나 vanishing gradient를 없앨지 층의 관점에서 학습시키는 것이다.

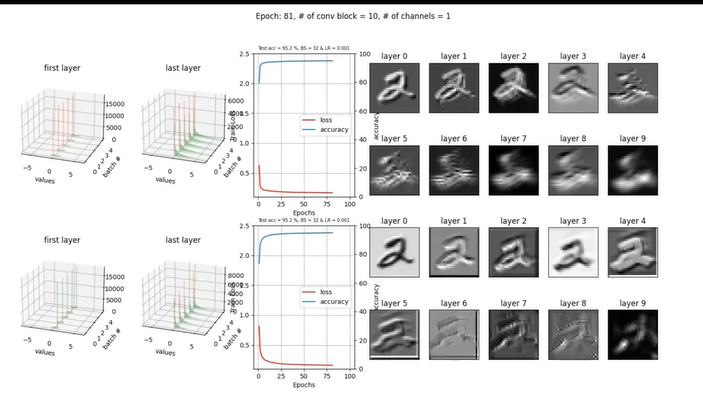
ReLU 활성화 함수 사용

위의 그림을 설명을 해주자면…
- 왼쪽에 있는 3차원 그래프는 0부터 4번 배치까지의 첫번째와 마지막 레이어에 들어간 데이터들의 분포를 히스토그램으로 나타낸 것이다.
- 이 예시에는 ReLU를 사용해서 이미 vanishing gradient를 없앤 상태이기 때문에 BN의 영향이 크지 않다.
- 성능 그래프에서도 큰 차이가 없고 분포의 차이도 거의 없는 것으로 보인다.,
- 즉, 이미 vanishing gradient가 해결된 경우는 BN이 의미가 없다.

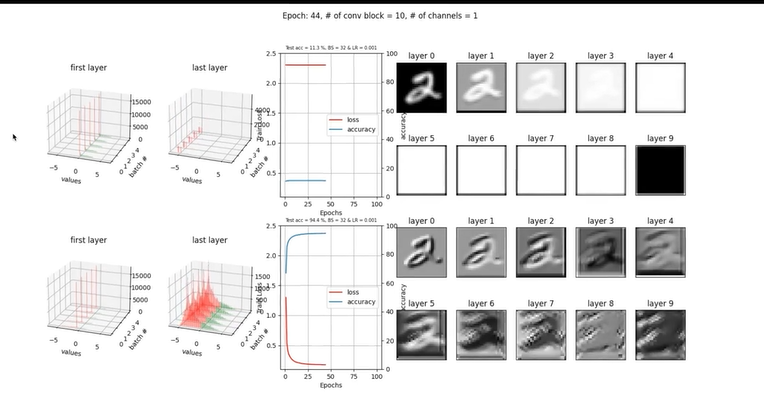
Sigmoid 활성화 함수 사용