Back Propagation
4-2. Back Propagation (역전파)
왜 역전파가 필요한가?
- 기본 선형 퍼셉트론에서는 $a$와 $b$에 대한 편미분. 즉, 2개의 편미분만 구하고 경사 하강법을 통해 파라미터의 값을 찾아갔다.
- 하지만 인공 신경망이 깊어질수록 학습해야 되는 파라미터의 갯수는 늘어나는데 이에 대한 편미분을 일일히 구하기에는 너무나 시간도 많이 들고 복잡해진다.
- 그래서 역전파라는 개념이 도입된 것이다.
역전파의 개념 이해
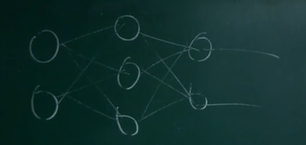
- 입력 층의 노드 : 2개
- 은닉 층의 갯수 : 1개
- 은닉 층의 노드 갯수 : 3개
-
출력 층의 노드 갯수 : 2개
- 위와 같은 인공 신경망이 있다고 가정하자.
- 출력 층의 첫번째 노드의 활성화 함수는 $f_2$, 노드의 들어가기 전의 값은 $d_2$, 노드 통과 후 값은 $n_2$ 은닉 층의 첫번째 노드에서 출력 층의 첫번째 노드로 갈 때의 가중치를 $W_2$라고 가정하자.
- 손실 함수는 MSE. 즉, 출력 값이 $\hat y_i$라고 할 때 $L = \sum\limits_i(\hat y_i - y_i)$ 이다.
- 손실 함수에 대해서 $W_2$의 편미분을 구해보자 (연쇄 법칙 사용)
- $\dfrac{\partial L}{\partial W_2} = \dfrac{\partial L}{\partial n_2}\dfrac{\partial n_2}{\partial d_2}\dfrac{\partial d_2}{\partial W_2} = 2(\hat y_1 - y_1)f’_2(d_2)n_1$
- 더 깊게 들어가서 은닉 층의 첫번째 노드의 활성화 함수는 $f_1$, 노드의 들어가기 전의 값은 $d_1$, 노드 통과 후 값은 $n_1$, 입력 층의 첫번째 노드에서 은닉 층의 첫번째 노드로 갈 때의 가중치를 $W_1$, 그리고 입력 층의 첫번째 노드 값을 $n_0$ 이라고 가정하자.
- 손실 함수에 대해서 $W_1$의 편미분을 구해보자
- $\dfrac{\partial L}{\partial W_1} = \dfrac{\partial L}{\partial n_2}\dfrac{\partial n_2}{\partial d_2}\dfrac{\partial d_2}{\partial n_1}\dfrac{\partial n_1}{\partial d_1}\dfrac{\partial d_1}{\partial W_1} = 2(\hat y_1 - y_1)f’_2(d_2)W_1f’_1(d_1)n_0$
- 위의 편미분의 차이점은 $W_2$에 대한 편미분이 아니라 은닉층 활성화 함수를 통과한 값인 $n_1$에 대해 편미분을 진행해주고 연쇄법칙을 진행하였다.
- 하지만 위에서의 편미분 값을 사실 잘못된 값이다.
- 은닉 층의 첫번째 노드를 통과하는 루트는 출력 층의 두번째 노드에서도 통과를 하기 때문에 이에 대한 루트에 대해서도 편미분을 구하여 더해주어야 정확한 편미분 값을 얻을 수 있다.
- 위와 같이 신경망이 깊어질수록 편미분에 대한 식이 길어지는데 이에 대한 패턴이 있다.
- 첫번째 값 즉, $2(\hat y_1-y_1)$은 손실 함수에 대한 고윳값이므로 손실 함수에 따라 달라진다.
- 이후로는 액, 웨, 액, 웨, …, 액, 앤
- 층 하나를 거친 편미분은 ‘액앤’으로 끝났고 층 두개를 거친 편미분은 ‘액웨액앤’으로 끝났다.
- 만약 층을 하나 더 거친다면 ‘액웨액웨액앤’의 형태의 편미분 값을 내놓을 것이다.
Forward Propagation (순전파)의 필요성
- 역전파를 진행하려면 순전파가 한번 시행되어야 한다.
- 왜냐하면 역전파에 쓰여지는 $d$값들은 순전파를 통해 계산이 되기 때문에 순전파를 진행하면서 $d$값을 기억해두고 역전파에 쓰인다.