Adam

3-8. Adam (Adaptive Moment Estimation)

Adam의 기본 개념

• Momentum과 RMSProp의 개념을 적절히 섞은 최적화 기법

Adam의 원리에 대한 이해

• $\theta_t \leftarrow \theta_{t-1}\alpha\dfrac{\hat m_t}{\sqrt{\hat v_t} + \epsilon}$
  • 이전에 살펴본 기본적인 파라미터 업데이트 공식과 큰 틀은 같다.
  • 마지막 항에 그라디언트 대신 새로운 식이 들어가있다.
  • 이 식만 해석하면 개념의 이해가 될 것.
• Adam 논문에서 주어준 초기 값들
  • $\alpha : \text{Step Size}$
  • $\beta_1,\beta_2 \in [0,1) : \text{Exponential decay rates for the moment estimates}$
  • $f(\theta) : \text{Stochastic objective function with parameters }\theta$
  • $\theta_0 : \text{Initial parameter vector}$
  • $m_0 = 0, v_0 = 0, t = 0$
• $m_t = \beta_1m_{t-1}+(1-\beta_1)g_t$
  • 예시로 식을 풀기 위해 $\beta_1,\beta_2=0.5$라고 가정
  • $m_1 = 0.5m_0 + 0.5g_1 \ = 0.5g_1$
  • $m_2 = 0.5 m_1+0.5g_2 \ = 0.5(0.5g_1)+0.5(g_2)$
  • $m_t$이라는 변수는 그라디언트를 누적해주는 변수. 즉, 모멘텀의 개념을 도입해주는 변수라고 볼수있다.
  • 이렇게 과거의 그라디언트의 기여도를 기하급수적으로 줄여나가며 과거의 잔재를 남기는 것을 Exponential Moving Average라고 한다.
• $v_t = \beta_2v_{t-1}+(1-\beta_2)g_t^2$
  • 이 또한 위의 식 풀이와 같이 Exponential Moving Average의 형태를 띄며 그라디언트를 누적해준다.
  • 하지만 그라디언트의 제곱 즉, 그라디언트의 크기를 누적하며 최종적으로 파라미터를 업데이트 할때 나누어주는 변수이기에 평준화를 시켜준다.
  • 그렇기에 $v_t$는 RMSProp의 개념을 도입해주는 변수이다.
• $\hat m_t = \dfrac{m_t}{(1-\beta_1^t)}, \hat v_t = \dfrac{v_t}{(1-\beta_2^t)}$
  • hat을 씌워주는 공식인데 간단하게 말하자면 $g_t$의 기댓값과 $m_t$의 기댓값을 비슷하게 만들어주고 $g_t^2$의 기댓값과 $v_t$의 기댓값을 비슷하게 만들어주는 과정이다.
  • 초기값이 0으로 계산되다 보니 초기에 Moving Average가 0 근처일수 밖에 없기 때문에 이 문제를 해결하기 위해 기댓값을 동일하게 만들어준다.
• $\epsilon$의 존재 이유
  • $\sqrt{\hat v_t}$는 그라디언트의 제곱이기 때문에 최소점에 도달할 수록 그라디언트는 0으로 수렴하기 시작한다.
  • 분모가 0으로 수렴하면 값이 갑자기 뛰기 때문에 이를 방지하기 위해 $\epsilon$라는 작은 양수를 도입한다.

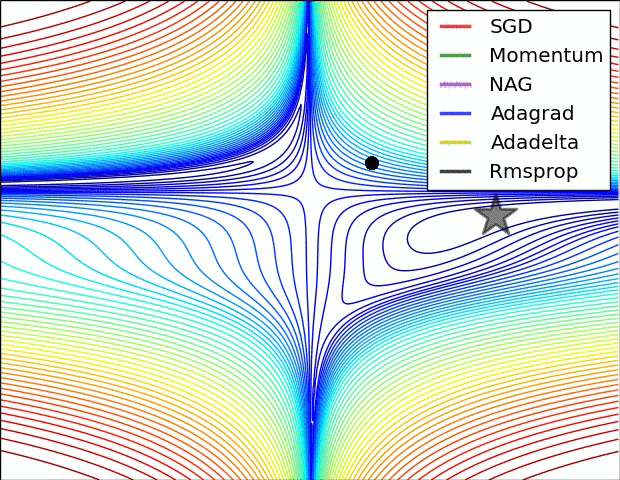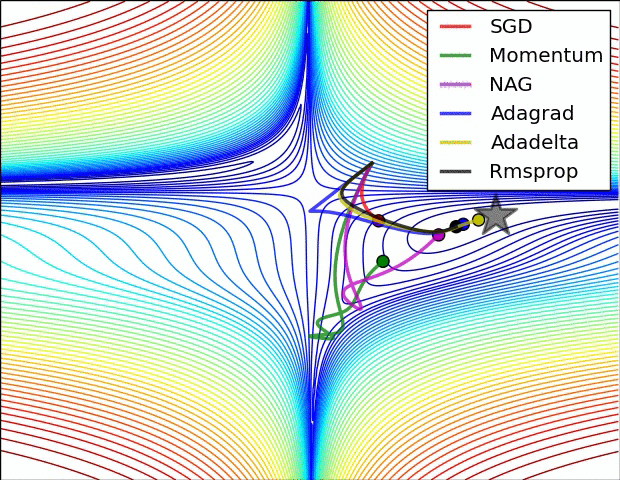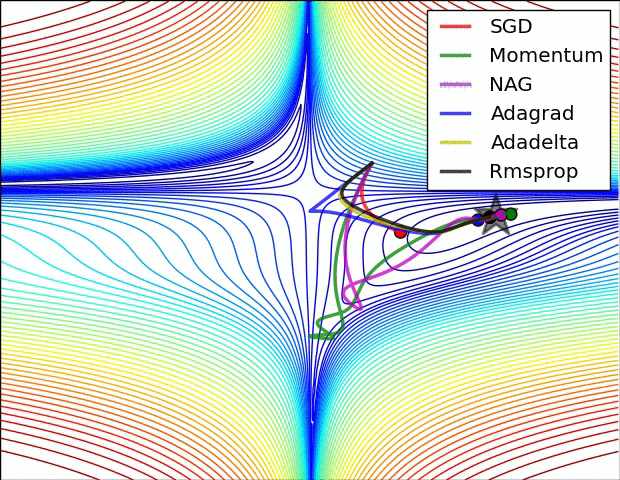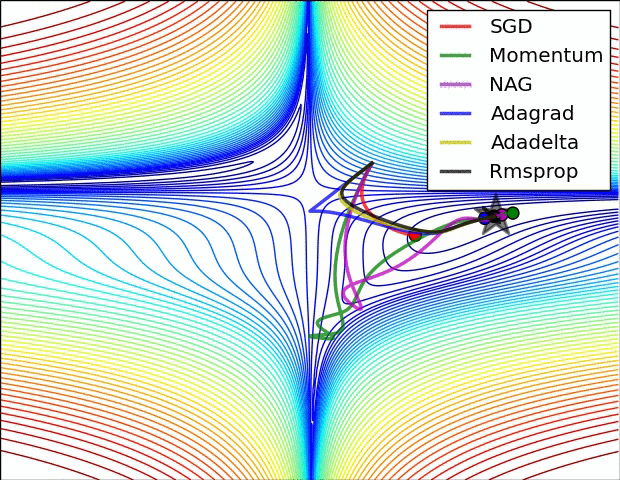
경사 하강법 최적화 기법의 시각화

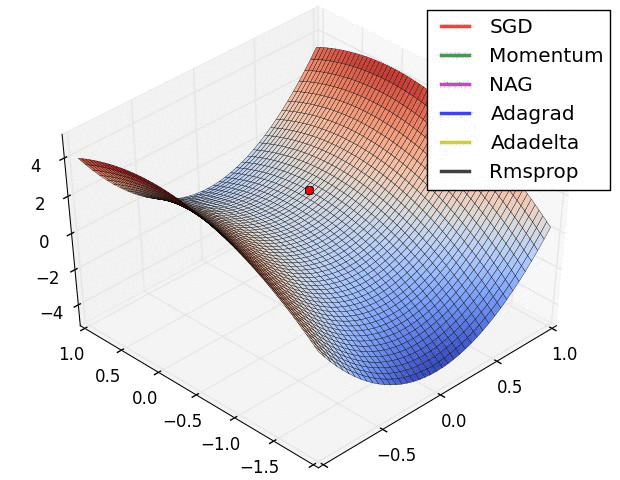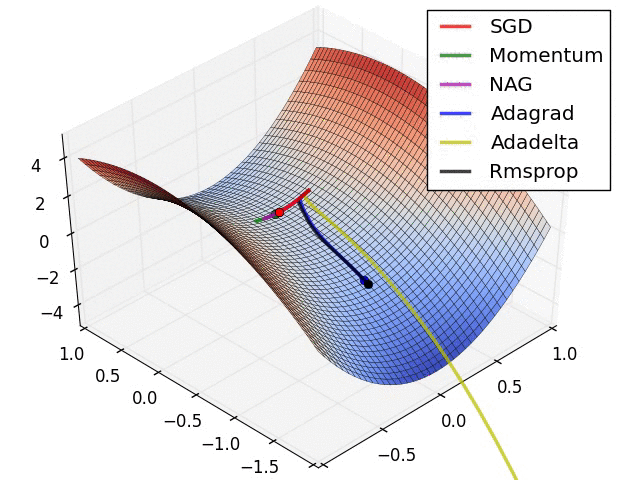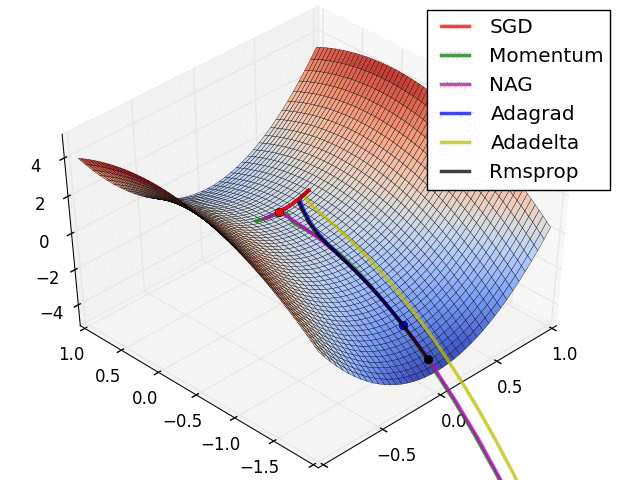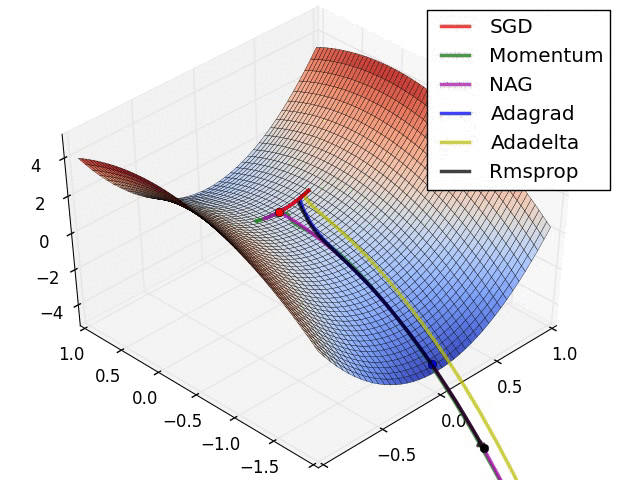
SGD는 Local Minimum에 갇혀서 빠져나오지 못하는 것을 볼수 있다. 그에 비해 RMSProp은 경사가 너무 심한 곳을 피하려다보니까 Local을 무사히 빠져나왔다.